
【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
(1)求证:PQ∥AB
(2)若点D在∠BAC的平分线上,求CP的长。
(3)若△PDE与△ABC重叠部分图形的周长为T,且12≤T≤16,求x的取值范围。
【答案】
(1)
证明:∵在Rt△ABC中,AB=15,BC=9,
∴AC=![]() =12.
=12.
∵![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() .
.
∵∠C=∠C,
∴△PQC∽△BAC,
∴∠CPQ=∠B,
∴PQ∥AB
(2)
解:连接AD,
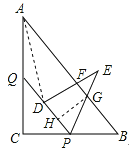
∵PQ∥AB,
∴∠ADQ=∠DAB.
∵点D在∠BAC的平分线上,
∴∠DAQ=∠DAB,
∴∠ADQ=∠DAQ,
∴AQ=DQ.
在Rt△CPQ中,PQ=5x,
∵PD=PC=3x,
∴DQ=2x.
∵AQ=12﹣4x,
∴12﹣4x=2x,解得x=2,
∴CP=3x=6.
(3)
解:当点E在AB上时,
∵PQ∥AB,
∴∠DPE=∠PEB.
∵∠CPQ=∠DPE,∠CPQ=∠B,
∴∠B=∠PEB,
∴PB=PE=5x,
∴3x+5x=9,解得x=![]() .
.
①当0<x≤![]() 时,T=PD+DE+PE=3x+4x+5x=12x,此时0<T≤
时,T=PD+DE+PE=3x+4x+5x=12x,此时0<T≤![]() ;
;
②当![]() <x<3时,设PE交AB于点G,DE交AB于F,作GH⊥FQ,垂足为H,
<x<3时,设PE交AB于点G,DE交AB于F,作GH⊥FQ,垂足为H,

∴HG=DF,FG=DH,Rt△PHG∽Rt△PDE,
∴![]() =
=![]() =
=![]() .
.
∵PG=PB=9﹣3x,
∴![]() =
=![]() =
=![]() ,
,
∴GH=![]() (9﹣3x),PH=
(9﹣3x),PH=![]() (9﹣3x),
(9﹣3x),
∴FG=DH=3x﹣![]() (9﹣3x),
(9﹣3x),
∴T=PG+PD+DF+FG=(9﹣3x)+3x+![]() (9﹣3x)+[3x﹣
(9﹣3x)+[3x﹣![]() (9﹣3x)]
(9﹣3x)]
=![]() x+
x+![]() ,
,
此时,![]() <T<18.
<T<18.
∴当0<x<3时,T随x的增大而增大,
∴T=12时,即12x=12,解得x=1;
TA=16时,即![]() x+
x+![]() =16,解得x=
=16,解得x=![]() .
.
∵12≤T≤16,
∴x的取值范围是1≤x≤![]() .
.
【解析】(1)先根据勾股定理求出AC的长,再由相似三角形的判定定理得出△PQC∽△BAC,由相似三角形的性质得出∠CPQ=∠B,由此可得出结论;
(2)连接AD,根据PQ∥AB可知∠ADQ=∠DAB,再由点D在∠BAC的平分线上,得出∠DAQ=∠DAB,故∠ADQ=∠DAQ,AQ=DQ.在Rt△CPQ中根据勾股定理可知,AQ=12﹣4x,故可得出x的值,进而得出结论;
(3)当点E在AB上时,根据等腰三角形的性质求出x的值,再分0<x≤![]() ;
;![]() <x<3两种情况进行分类讨论.
<x<3两种情况进行分类讨论.
此题考查了几何图形的折叠问题,涉及的几何知识有勾股定理,相似三角形的判定定理和等腰三角形的性质等。


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD. 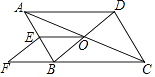
(1)求证;四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由大小两种货车,3辆大车与4辆小车一次可以运货22吨,2辆大车与6辆小车一次可以运货23吨.请根据以上信息,提出一个能用方程(组)解决的问题,并写出这个问题的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图:
(1)本次检测抽取了大、中、小学生共 名,其中小学生 名.
(2)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为 名.
(3)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.
等级 | 人数/名 |
优秀 | a |
良好 | b |
及格 | 150 |
不及格 | 50 |
解答下列问题:
(1)a= ,b=
(2)补全条形统计图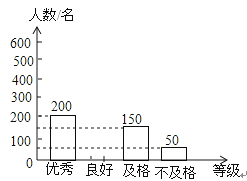
(3)试估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有2个相同的小球,它们分别写有数字1和2;乙口袋中装有3个相同的小球,它们分别写有数字3,4和5,从两个口袋中各随机取出1个小球.用画树状图或列表的方法,求取出的2个小球上的数字之和为6的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 的图象经过点A(﹣3,﹣2).
的图象经过点A(﹣3,﹣2).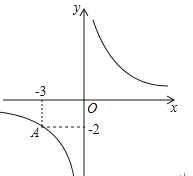
(1)求反比例函数的解析式;
(2)若点B(1,m),C(3,n)在该函数的图象上,试比较m与n的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com