
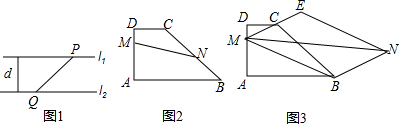
分析 (1)根据垂线段最短得:PQ长度的最小值为:l1和l2的距离;
(2)如图2,当MN⊥BC时,MN的值最小,证明△EMN是等腰直角三角形,先根据AM=3MD,求DM的长,证明△EDC∽△EAB,得ED=2,则EM=3,所以可得MN的长;
(3)作辅助线,构建相似三角形,先根据平行线分线段成比例定理得:$\frac{CG}{BG}=\frac{1}{2}$,G是BC上一定点,得出
当MN⊥AD时,MN的长最小,计算AH的长就是MN的最小值.
解答  解:(1)∵直线l1∥l2,l1和l2的距离为d,
解:(1)∵直线l1∥l2,l1和l2的距离为d,
∴PQ长度的最小值为d;
故答案为:d;
(2)如图2,∵AD=4,AM=3DM,
∴AM=3,DM=1,
延长AD、BC交于E,
当MN⊥BC时,MN的值最小,
∵DC∥AB,
∴△EDC∽△EAB,
∴$\frac{ED}{EA}=\frac{DC}{AB}$,
∴$\frac{ED}{ED+4}=\frac{2}{6}$,
∴ED=2,
∴ED=DC=2,
∴△EDC是等腰直角三角形,
∴∠E=45°,
∴△EMN是等腰直角三角形,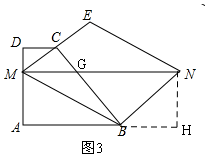
∵EM=3,
∴MN=$\frac{3}{\sqrt{2}}$=$\frac{3}{2}\sqrt{2}$;
(3)当MN⊥AD时,MN的长最小,
∴MN∥DC∥AB,
∴∠DCM=∠CMN=∠MNB=∠NBH,
设MN与BC相交于点G,
∵ME∥BN,MC=CE,
∴$\frac{CG}{BG}=\frac{1}{2}$,
∴G是BC上一定点,
作NH⊥AB,交AB的延长线于H,
∵∠D=∠H=90°,
∴Rt△MDC∽Rt△NHB,
即$\frac{DC}{HB}$=$\frac{1}{2}$,
∴BH=2DC=4,
∴AH=AB+BH=6+4=10,
∴当MN⊥AD时,MN的长最小,即为10;
则线段MN长度的最小值为10.
点评 本题是四边形的综合题,考查了平行四边形的性质、相似三角形的判定与性质、直角梯形的性质、矩形、平行四边形的性质、垂线段最短,注意准确作出辅助线是解此题的关键,本题还运用了类比的思想解决问题.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:选择题
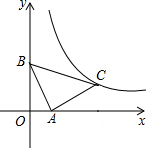 如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别交于A、B两点,△BAC为等腰直角三角形,且∠BAC=90°.若点C恰好落在函数y=$\frac{k}{x}$(x>0)在第一象限内的图象上,则k的值为( )
如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别交于A、B两点,△BAC为等腰直角三角形,且∠BAC=90°.若点C恰好落在函数y=$\frac{k}{x}$(x>0)在第一象限内的图象上,则k的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 没有实数根 | B. | 只有一个实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
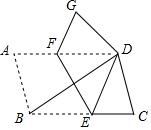 在?ABCD中,∠DBC=32°,现将?ABCD沿EF折叠,使点B与点D重合,点A落在G处,则∠GFE的度数( )
在?ABCD中,∠DBC=32°,现将?ABCD沿EF折叠,使点B与点D重合,点A落在G处,则∠GFE的度数( )| A. | 132° | B. | 122° | C. | 112° | D. | 102° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com