
| 1 |
| 2 |
| 1 |
| 2 |
| AB2-MB2 |
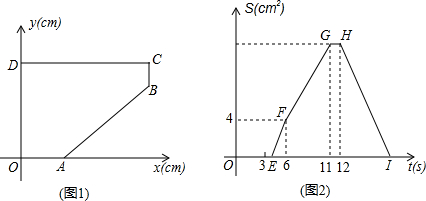
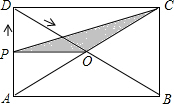
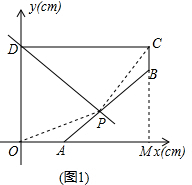 (2)因为P在OA、BC、CD上时,直线PD都不能将五边形OABCD分成面积相等的两部分,
(2)因为P在OA、BC、CD上时,直线PD都不能将五边形OABCD分成面积相等的两部分,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 由
由
|
| 42 |
| 11 |
| 15 |
| 11 |
| 42 |
| 11 |
| 15 |
| 11 |
| 15 |
| 11 |
| 42 |
| 11 |
| 29 |
| 42 |
| 29 |
| 42 |



科目:初中数学 来源:不详 题型:单选题
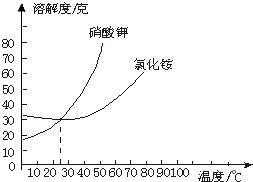
| A.硝酸钾的溶解度比氯化铵的溶解度大 |
| B.约26℃时二者的溶解度相等 |
| C.温度为10℃时氯化铵的溶解度大 |
| D.温度为40℃时,硝酸钾的溶解度大 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A.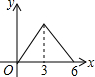 | B.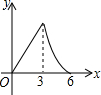 | C.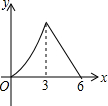 | D.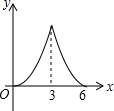 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A.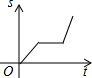 | B.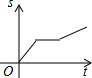 | C.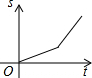 | D.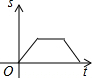 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 船在水深不低于6米时可安全通航,满足这一要求的时间段是( )
船在水深不低于6米时可安全通航,满足这一要求的时间段是( )| A.12小时以后 | B.14小时以后 | C.10时到14时 | D.12时到16时 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
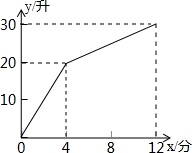
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com