
分析 利用规定的运算方法,分别算得a1,a2,a3,a4…找出运算结果的循环规律,利用规律解决问题.
解答 解:∵a1=-3,
a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{1-(-3)}$=$\frac{1}{4}$,
a3=$\frac{1}{1-{a}_{2}}$=$\frac{1}{1-\frac{1}{4}}$=$\frac{4}{3}$,
a4=$\frac{1}{1-{a}_{3}}$=$\frac{1}{1-\frac{4}{3}}$=-3,
…
数列以-3,$\frac{1}{4}$,$\frac{4}{3}$三个数依次不断循环,
∵2016÷3=672,
∴a2016=a3=$\frac{4}{3}$,
故答案为:$\frac{4}{3}$.
点评 本题是对数字变化规律的考查,理解差倒数的定义并求出每3个数为一个循环组依次循环是解题的关键.


科目:初中数学 来源: 题型:解答题
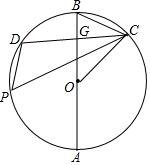 在⊙O中,直径AB⊥CD于点G(CD为非直径弦),P是⊙O上一动点(不考虑点P与C,D重合的情况)
在⊙O中,直径AB⊥CD于点G(CD为非直径弦),P是⊙O上一动点(不考虑点P与C,D重合的情况)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
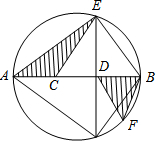 如图,半径为3cm的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连接AE,BF,则图中两个阴影部分的面积为$\frac{3\sqrt{11}}{2}$.
如图,半径为3cm的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连接AE,BF,则图中两个阴影部分的面积为$\frac{3\sqrt{11}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
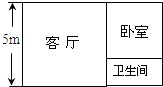 如图,有一长方形的仓库,一边长为5m,现要将它改建为简易住房,改建后的住房分为客厅、卧室和卫生间三部分,其中客厅和卧室都为正方形,且卧室的面积大于卫生间的面积,若改建后卫生间的面积为6m2,则长方形仓库另一边的长是8m.
如图,有一长方形的仓库,一边长为5m,现要将它改建为简易住房,改建后的住房分为客厅、卧室和卫生间三部分,其中客厅和卧室都为正方形,且卧室的面积大于卫生间的面积,若改建后卫生间的面积为6m2,则长方形仓库另一边的长是8m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com