
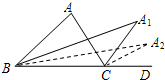
 如图,已知△ABC的内角∠A=a,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A2016,则∠A2016的度数是$\frac{α}{{2}^{2016}}$.
如图,已知△ABC的内角∠A=a,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A2016,则∠A2016的度数是$\frac{α}{{2}^{2016}}$. 分析 根据角平分线的定义可得∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,整理即可求出∠A1的度数,同理求出∠A2,可以发现后一个角等于前一个角的$\frac{1}{2}$,根据此规律即可得解.
解答 解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠ABC+∠A1,
∴∠A1=$\frac{1}{2}$∠A,
∵∠A=α,
∴∠A1=$\frac{α}{2}$;
同理可得∠A2=$\frac{1}{2}$∠A1=$\frac{1}{2}$•$\frac{1}{2}$α=$\frac{α}{{2}^{2}}$,
∴∠An=$\frac{α}{{2}^{n}}$,
∴∠A2016=$\frac{α}{{2}^{2016}}$.
故答案为:$\frac{α}{{2}^{2016}}$
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.


科目:初中数学 来源: 题型:解答题
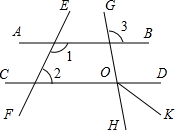 已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.
已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60 | B. | 30 | C. | 20 | D. | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com