
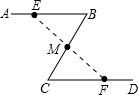
 如图、公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E,F,M,且BE=CF,M在BC的中点,试判断三只石凳E,M,F恰好在一直线上吗?为什么?
如图、公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E,F,M,且BE=CF,M在BC的中点,试判断三只石凳E,M,F恰好在一直线上吗?为什么? 分析 先根据SAS判定△BEM≌△CFM,从而得出∠BME=∠CMF.通过角之间的转换可得到E,M,F在一条直线上.
解答 证明:连接ME,MF.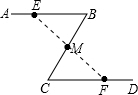
∵AB∥CD,(已知)
∴∠B=∠C(两线平行内错角相等).
在△BEM和△CFM中,$\left\{\begin{array}{l}{EB=CF}\\{∠B=∠C}\\{MB=CM}\end{array}\right.$,
∴△BEM≌△CFM(SAS).
∴∠BME=∠CMF,
∴∠EMF=∠BME+∠BMF=∠CMF+∠BMF=∠BMC=180°,
∴E,M,F在一条直线上.
点评 此题主要考查了全等三角形的应用,关键是掌握判定两个三角形全等的判定方法,注意共线的证明方法.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
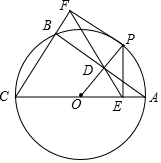 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线ED交CB的延长线于F点,连接PF.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线ED交CB的延长线于F点,连接PF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
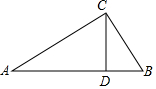 如图,在 Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:
如图,在 Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
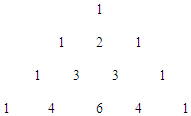 我们已经知道:
我们已经知道:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com