
分析 (1)设2012年底至2014年底该市汽车拥有量的年平均增长率是x,根据2012年底该市汽车拥有量为100万辆,而截止到2014年底,该市的汽车拥有量已达144万辆可列方程求解.
(2)设2014年底到2015年底该市汽车拥有量的年平均增长率为y,则2015年底全市的汽车拥有量为144(1+y)×90%万辆,根据要求到2015年底全市汽车拥有量不超过155.52万辆可列不等式求解.
解答 解:(1)设2010年底至2012年底该市汽车拥有量的年平均增长率是x,
根据题意,100(1+x)2=144
1+x=±1.2
∴x1=0.2=20% x2=-2.2(不合题意,舍去),
答:2010年底至2012年底该市汽车拥有量的年平均增长率是20%.
(2)设2012年底到2013年底该市汽车拥有量的年平均增长率为y,
根据题意得:144(1+y)-144×10%≤155.52,
解得:y≤0.18,
答:2012年底至2013年底该市汽车拥有量的年增长率要控制在不超过18%能达到要求.
点评 本题考查了一元二次方程的应用及不等式的应用,重点考查理解题意的能力,根据增长的结果做为等量关系列出方程求解,根据2015车的总量这个不等量关系列出不等式求解.


科目:初中数学 来源: 题型:解答题
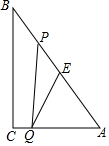 如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从 B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当 点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.
如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从 B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当 点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
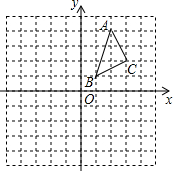 如图,在平面直角坐标系中,A(2,4),B(1,1),C(3,2).
如图,在平面直角坐标系中,A(2,4),B(1,1),C(3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减(单位:个) | +5 | -2 | -5 | +15 | -10 | +12 | -9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com