
ЁОЬтФПЁПзлКЯгыЬНОПЃЎ
ШчЭМ1ЃЌХзЮяЯпyЃН![]() x2Љ
x2Љ![]() xЉ2гыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌОЙ§ЕуBЕФжБЯпНЛyжсгкЕуEЃЈ0ЃЌ2ЃЉЃЎ
xЉ2гыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌОЙ§ЕуBЕФжБЯпНЛyжсгкЕуEЃЈ0ЃЌ2ЃЉЃЎ
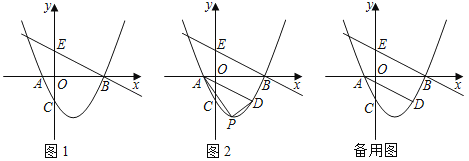
ЃЈ1ЃЉЧѓAЃЌBЃЌCШ§ЕуЕФзјБъМАжБЯпBEЕФНтЮіЪНЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуAзїBEЕФЦНааЯпНЛХзЮяЯпгкЕуDЃЌЕуPЪЧХзЮяЯпЩЯЮЛгкЯпЖЮADЯТЗНЕФвЛИіЖЏЕуЃЌСЌНгPAЃЌPDЃЌЧѓOAPDУцЛ§ЕФзюДѓжЕЃЎ
ЃЈ3ЃЉШєЃЈ2ЃЉжаЕФЕуPЮЊХзЮяЯпЩЯвЛЖЏЕуЃЌдкxжсЩЯЪЧЗёДцдкЕуQЃЌЪЙЕУвдAЃЌDЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ2ЃЉЃЛyЃНЉ![]() x+2ЃЛ(2) 4ЃЛ(3)ДцдкЃЛЕуQЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЛђЃЈЉ4ЃЌ0ЃЉЛђЃЈ
x+2ЃЛ(2) 4ЃЛ(3)ДцдкЃЛЕуQЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЛђЃЈЉ4ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉСюy=0ПЩЧѓAгыBЕузјБъЃЌСюx=0ПЩЧѓГіCЕуЕФзјБъЃЛЩшжБЯпBEЕФНтЮіЪНЮЊy=kx+bЃЌНЋBЃЈ4ЃЌ0ЃЉЁЂEЃЈ0ЃЌ2ЃЉДњШыНтЮіЪНПЩЧѓkгыbЕФжЕЃЛ
ЃЈ2ЃЉЩшADЕФНтЮіЪНЮЊy=-![]() x+mЃЌНЋAЃЈ-1ЃЌ0ЃЉДњШыЧѓГіmЃЌНјЖјШЗЖЈжБЯпADЕФНтЮіЪНЃЌдйСЊСЂ
x+mЃЌНЋAЃЈ-1ЃЌ0ЃЉДњШыЧѓГіmЃЌНјЖјШЗЖЈжБЯпADЕФНтЮіЪНЃЌдйСЊСЂ ЧѓГіDЕузјБъЃЌЙ§ЕуPзїPFЁЭxжсгкЕуFЃЌНЛADгкЕуNЃЌЙ§ЕуDзїDGЁЭxжсгкЕуGЃЎдђSЁїAPD=SЁїAPN+SЁїDPN=2PNЃЌЩшP
ЧѓГіDЕузјБъЃЌЙ§ЕуPзїPFЁЭxжсгкЕуFЃЌНЛADгкЕуNЃЌЙ§ЕуDзїDGЁЭxжсгкЕуGЃЎдђSЁїAPD=SЁїAPN+SЁїDPN=2PNЃЌЩшP![]() ЃЌдђN
ЃЌдђN![]() ЃЌЧѓГіPN=-
ЃЌЧѓГіPN=-![]() a2+a+
a2+a+![]() ЃЌЫљвдSЁїAPD=-a2+2a+3=-ЃЈa-1ЃЉ2+4ЃЌЕБa=1ЪБЃЌЁїAPDЕФУцЛ§зюДѓЃЌзюДѓжЕЮЊ4ЃЛ
ЃЌЫљвдSЁїAPD=-a2+2a+3=-ЃЈa-1ЃЉ2+4ЃЌЕБa=1ЪБЃЌЁїAPDЕФУцЛ§зюДѓЃЌзюДѓжЕЮЊ4ЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЬжТлЃКЂйЕБPDгыAQЮЊЦНааЫФБпаЮЕФЖдБпЪБЃЌгЩPD=AQ=3ЃЌПЩЧѓQЃЈ2ЃЌ0ЃЉЛђQЃЈ-4ЃЌ0ЃЉЃЛЂкЕБPDгыAQЮЊЦНааЫФБпаЮЕФЖдНЧЯпЪБЃЌЯШЧѓГіP ЛђP
ЛђP ЃЌдйЧѓГіPDЕФжаЕуЮЊ
ЃЌдйЧѓГіPDЕФжаЕуЮЊ Лђ
Лђ ЃЌгЩЦНааЫФБпаЮЖдНЧЯпЕФаджЪПЩЧѓQ
ЃЌгЩЦНааЫФБпаЮЖдНЧЯпЕФаджЪПЩЧѓQ ЛђQ
ЛђQ ЃЎ
ЃЎ
НтЃКЃЈ1ЃЉСюyЃН0ЃЌдђ![]() x2Љ
x2Љ![]() xЉ2ЃН0ЃЌНтЕУxЃН4ЛђxЃНЉ1ЃЌ
xЉ2ЃН0ЃЌНтЕУxЃН4ЛђxЃНЉ1ЃЌ
ЁрAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌ
СюxЃН0ЃЌдђyЃНЉ2ЃЌЁрCЃЈ0ЃЌЉ2ЃЉЃЌ
ЩшжБЯпBEЕФНтЮіЪНЮЊyЃНkx+bЃЌ
НЋBЃЈ4ЃЌ0ЃЉЁЂEЃЈ0ЃЌ2ЃЉДњШыЕУЃЌ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК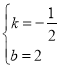 ЃЌ
ЃЌ
ЁрyЃНЉ![]() x+2ЃЛ
x+2ЃЛ
ЃЈ2ЃЉгЩЬтвтПЩЩшADЕФНтЮіЪНЮЊyЃНЉ![]() x+mЃЌ
x+mЃЌ
НЋAЃЈЉ1ЃЌ0ЃЉДњШыЃЌЕУЕНmЃНЉ![]() ЃЌ
ЃЌ
ЁрyЃНЉ![]() xЉ
xЉ![]() ЃЌ
ЃЌ
СЊСЂ ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрDЃЈ3ЃЌЉ2ЃЉЃЌ
Й§ЕуPзїPFЁЭxжсгкЕуFЃЌНЛADгкЕуNЃЌЙ§ЕуDзїDGЁЭxжсгкЕуGЃЎ

ЁрSЁїAPDЃНSЁїAPN+SЁїDPNЃН![]() PNAF+
PNAF+![]() PNFGЃН
PNFGЃН![]() PNЃЈAF+FGЃЉЃН
PNЃЈAF+FGЃЉЃН![]() PNAGЃН
PNAGЃН![]() ЁС4PNЃН2PNЃЌ
ЁС4PNЃН2PNЃЌ
ЩшPЃЈaЃЌЉ![]() a2Љ
a2Љ![]() aЉ2ЃЉЃЌдђNЃЈaЃЌЉ
aЉ2ЃЉЃЌдђNЃЈaЃЌЉ![]() aЉ
aЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрPNЃНЉ![]() a2+a+
a2+a+![]() ЃЌ
ЃЌ
ЁрSЁїAPDЃНЉa2+2a+3ЃНЉЃЈaЉ1ЃЉ2+4ЃЌ
ЁпЉ1ЃМ0ЃЌЉ1ЃМaЃМ3ЃЌ
ЁрЕБaЃН1ЪБЃЌЁїAPDЕФУцЛ§зюДѓЃЌзюДѓжЕЮЊ4ЃЛ
ЃЈ3ЃЉДцдкЃЛ
ЂйЕБPDгыAQЮЊЦНааЫФБпаЮЕФЖдБпЪБЃЌ
ЁпAQЁЮPDЃЌAQдкxжсЩЯЃЌ
ЁрPЃЈ0ЃЌЉ2ЃЉЃЌ
ЁрPDЃН3ЃЌ
ЁрAQЃН3ЃЌ
ЁпAЃЈЉ1ЃЌ0ЃЉЃЌ
ЁрQЃЈ2ЃЌ0ЃЉЛђQЃЈЉ4ЃЌ0ЃЉЃЛ
ЂкЕБPDгыAQЮЊЦНааЫФБпаЮЕФЖдНЧЯпЪБЃЌ
PDгыAQЕФжаЕудкxжсЩЯЃЌ
ЁрPЕуЕФзнзјБъЮЊ2ЃЌ
ЁрPЃЈ![]() ЃЌ2ЃЉЛђPЃЈ
ЃЌ2ЃЉЛђPЃЈ![]() ЃЌ2ЃЉЃЌ
ЃЌ2ЃЉЃЌ
ЁрPDЕФжаЕуЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЁпQЕугыAЕуЙигкPDЕФжаЕуЖдГЦЃЌ
ЁрQЃЈ![]() ЃЌ0ЃЉЛђQЃЈ
ЃЌ0ЃЉЛђQЃЈ![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
злЩЯЫљЪіЃКЕуQЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЛђЃЈЉ4ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ


 ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ
ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОиаЮABCDжаЃЌЖдНЧЯпACЁЂBDНЛгкЕуOЃЌAEЁЭBDгкEЃЌЁЯCAEЃН10ЁуЃЌдђЁЯADBЃН_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ЁАСљвЛЁБЧАЯІжЪМрВПУХДгФГГЌЪаОЯњЕФЖљЭЏЭцОпЁЂЭЏГЕКЭЭЏзАжаЙВГщВщСЫ300МўЖљЭЏгУЦЗЃЌвдЯТЪЧИљОнГщВщНсЙћЛцжЦГіЕФВЛЭъећЕФЭГМЦБэКЭЩШаЮЭМЃЛ
РрБ№ | ЖљЭЏЭцОп | ЭЏГЕ | ЭЏзА |
ГщВщМўЪ§ | 90 |

ЧыИљОнЩЯЪіЭГМЦБэКЭЩШаЮЬсЙЉЕФаХЯЂЃЌЭъГЩЯТСаЮЪЬтЃК
ЃЈ1ЃЉЗжБ№ВЙШЋЩЯЪіЭГМЦБэКЭЭГМЦЭМЃЛ
ЃЈ2ЃЉвбжЊЫљГщВщЕФЖљЭЏЭцОпЁЂЭЏГЕЁЂЭЏзАЕФКЯИёТЪЗжБ№ЮЊ90%ЁЂ88%ЁЂ80%ЃЌШєДгИУГЌЪаЕФетШ§РрЖљЭЏгУЦЗжаЫцЛњЙКТђвЛМўЃЌТђЕНКЯИёЦЗЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() гы
гы![]() жсЁЂ
жсЁЂ![]() жсЗжБ№НЛгкЕу
жсЗжБ№НЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌНЋЕу
ЃЌНЋЕу![]() ЯђгвЦНвЦ5ИіЕЅЮЛГЄЖШЃЌЕУЕНЕу
ЯђгвЦНвЦ5ИіЕЅЮЛГЄЖШЃЌЕУЕНЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФЖдГЦжсЃЛ
ЃЈ3ЃЉШєХзЮяЯпгыЯпЖЮ![]() ЧЁгавЛИіЙЋЙВЕуЃЌНсКЯКЏЪ§ЭМЯѓЃЌЧѓ
ЧЁгавЛИіЙЋЙВЕуЃЌНсКЯКЏЪ§ЭМЯѓЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃПЊеЙвдЁАЮвУЧЖМЪЧзЗУЮШЫЁБЮЊжїЬтЕФаЃдАЮФЛЏНкЛюЖЏЃЌЛюЖЏЗжЮЊЧђРрЁЂЪщЛЁЂРжЦїЁЂЫаЖСЫФЯюФкШнЃЌвЊЧѓУПЮЛбЇЩњВЮМгЦфжаЕФвЛЯюЃЎаЃбЇЩњЛсЮЊСЫНтИїЯюБЈУћЧщПіЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјааЕїВщЃЌВЂЖдЕїВщНсЙћНјааСЫЭГМЦЃЌЛцжЦСЫШчЯТЭГМЦЭМЃЈОљВЛЭъећЃЉЃК

ЧыНтД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉЭМ1жаЃЌЁАЪщЛЁБетвЛЯюЕФШЫЪ§ЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉЭМ2жаЃЌЁАРжЦїЁБетвЛЯюЕФАйЗжБШЪЧЁЁ ЁЁЃЌЁАЧђРрЁБетвЛЯюЫљЖдгІЕФЩШаЮЕФдВаФНЧЖШЪ§ЪЧЁЁ ЁЁЃЎ
ЃЈ3ЃЉШєИУаЃЙВга2200УћбЇЩњЃЌЧыЙРМЦИУаЃВЮМгЁАЫаЖСЁБетвЛЯюЕФбЇЩњдМгаЖрЩйШЫЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉМЦЫуЃКЃЈЉ3ЃЉ2ЉЃЈІаЉ4ЃЉ0+ЃЈ![]() ЃЉЉ2ЃЛ
ЃЉЉ2ЃЛ
ЃЈ2ЃЉЃЈa+2ЃЉ2+ЃЈ1ЉaЃЉЃЈ1+aЃЉЃЎ
ЃЈ3ЃЉНтЗНГЬЃК![]() ЃН
ЃН![]() ЃЛ
ЃЛ
ЃЈ4ЃЉНтВЛЕШЪНзщЃК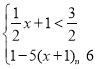
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮ ABCD ЕФЖдНЧЯп AC гы BD НЛгкЕу OЃЌЕу E дк AD ЩЯЃЌЧв DE=CDЃЌСЌНг OEЃЌBEЃЌ ABE ![]() ACB ЃЌШє AE=2ЃЌдђ OE ЕФГЄЮЊ___________ЃЎ
ACB ЃЌШє AE=2ЃЌдђ OE ЕФГЄЮЊ___________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊХфКЯЮвЪаЁАДДНЈШЋЙњЮФУїГЧЪаЁБФГЕЅЮЛМЦЛЎдквЛПщОиаЮПеЕиЩЯаоНЈТЬЩЋжВЮядАЃЈШчЭМЫљЪОЃЉЃЌЦфжаБпППЧНЃЈЧНГЄЮЊ![]() УзЃЉЃЌСэЭтШ§БпгУзмГЄ36УзЕФВФСЯЮЇГЩЃЎШє
УзЃЉЃЌСэЭтШ§БпгУзмГЄ36УзЕФВФСЯЮЇГЩЃЎШє![]() УзЃЌОиаЮ
УзЃЌОиаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЦНЗНУзЃЎ
ЦНЗНУзЃЎ
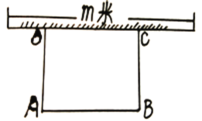
ЃЈ1ЃЉЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєОиаЮУцЛ§ЮЊ160ЦНЗНУзЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЧАЬсЯТЃЌЧНГЄ![]() УзЖд
УзЖд![]() ЕФГЄгагАЯьТ№ЃПЧыЯъЯИЫЕУїЃЎ
ЕФГЄгагАЯьТ№ЃПЧыЯъЯИЫЕУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЩшЕуPЃЈx1ЃЌy1ЃЉЃЌQЃЈx2ЃЌy2ЃЉЪЧЭМаЮWЩЯЕФШЮвтСНЕуЃЎ
ЖЈвхЭМаЮWЕФВтЖШУцЛ§ЃКШє|x1Љx2|ЕФзюДѓжЕЮЊmЃЌ|y1Љy2|ЕФзюДѓжЕЮЊnЃЌдђS=mnЮЊЭМаЮWЕФВтЖШУцЛ§ЃЎ
Р§ШчЃЌШєЭМаЮWЪЧАыОЖЮЊ1ЕФЁбOЃЌЕБPЃЌQЗжБ№ЪЧЁбOгыxжсЕФНЛЕуЪБЃЌШчЭМ1ЃЌ|x1Љx2|ШЁЕУзюДѓжЕЃЌЧвзюДѓжЕm=2ЃЛЕБPЃЌQЗжБ№ЪЧЁбOгыyжсЕФНЛЕуЪБЃЌШчЭМ2ЃЌ|y1Љy2|ШЁЕУзюДѓжЕЃЌЧвзюДѓжЕn=2ЃЎдђЭМаЮWЕФВтЖШУцЛ§S=mn=4
ЃЈ1ЃЉШєЭМаЮWЪЧЕШбќжБНЧШ§НЧаЮABOЃЌOA=OB=1ЃЎ
ЂйШчЭМ3ЃЌЕБЕуAЃЌBдкзјБъжсЩЯЪБЃЌЫќЕФВтЖШУцЛ§S= ЃЛ
ЂкШчЭМ4ЃЌЕБABЁЭxжсЪБЃЌЫќЕФВтЖШУцЛ§S= ЃЛ
ЃЈ2ЃЉШєЭМаЮWЪЧвЛИіБпГЄ1ЕФе§ЗНаЮABCDЃЌдђДЫЭМаЮЕФВтЖШУцЛ§SЕФзюДѓжЕЮЊ ЃЛ
ЃЈ3ЃЉШєЭМаЮWЪЧвЛИіБпГЄЗжБ№ЮЊ3КЭ4ЕФОиаЮABCDЃЌЧѓЫќЕФВтЖШУцЛ§SЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com