分析:
(1)若一元二次方程有实数根,则根的判别式△=b2-4ac≥0,建立关于k的不等式,即可求出k的取值范围.
(2)由于AB=2是方程kx2-4x+2=0,所以可以确定k的值,进而再解方程求出BC的值。
解答:
(1)∵方程有实数根,
∴△=b2-4ac=(-4)2-4×k×2=16-8k≥0,
解得:k≤2,
又因为k是二次项系数,所以k≠0,
所以k的取值范围是k≤2且k≠0。
(2)由于AB=2是方程kx2-4x+2=0,
所以把x=2代入方程,可得k=3/2,
所以原方程是:3x2-8x+4=0,
解得:x1=2,x2=2/3,
所以BC的值是2/3。
点评:本题主要考查了一元二次方程的根的判别式的应用,容易出现的错误是忽视根的判别式应用的前提条件:二次项系数k≠0。

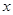 的一元二次方程
的一元二次方程 有实数根.
有实数根. 的取值范围.
的取值范围.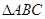 中,
中,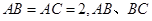 的长是方程
的长是方程 的两根,求
的两根,求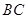 的长.
的长.

