
 如图,已知抛物线y=x2-2(m+1)x+m2+1与x轴的相交于A,B两点,与y轴交于C(0,5)点,O为原点.
如图,已知抛物线y=x2-2(m+1)x+m2+1与x轴的相交于A,B两点,与y轴交于C(0,5)点,O为原点.分析 (1)用待定系数法求二次函数解析式.并令抛物线的解析式中y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标即可.
(2)存在.分①当∠OQP=∠OCB时,△OCB∽△OQP,②当∠OCB=∠OPQ时,△COB∽△POQ两种情况讨论.
解答 解:(1)∵抛物线y=x2-2(m+1)x+m2+1与y轴交于C(0,5)点,
∴5=m2+1.m=±2
当m=2时,抛物线y=x2-6x+5;
+m2+1当m=-2时,抛物线y=x2+2x+5,此时抛物线与x轴无交点,故不符合题意,舍去.
令x2-6x+5=0,(x-1)(x-5)=0,∴x1=1,x2=5
∴A(1,0),B(5,0)
即:抛物线的解析式为:y=x2-6x+5;A,B两点的坐标分别为:A(1,0),B(5,0).
(2)存在.如下图所示:
①当∠OQP=∠OCB时,△OCB∽△OQP,
∴$\frac{OC}{OQ}=\frac{OB}{OP}$,$\frac{5}{t}=\frac{1}{5-t}$,解之得:t=$\frac{25}{6}$(秒)
②当∠OCB=∠OPQ时,△COB∽△POQ,
∴$\frac{CO}{OP}=\frac{OB}{OQ}$,$\frac{5}{5-t}=\frac{1}{t}$,解之得:t=$\frac{5}{6}$$\frac{25}{6}$
即:当t等于$\frac{5}{6}$秒或$\frac{25}{6}$秒时,以O,P,Q为顶点的三角形与△OBC相似.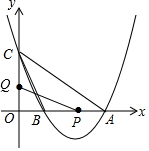
点评 本题考查了相似三角形的判定与性质、待定系数法求二次函数解析式、抛物线与x轴的交点等问题,解题的关键是熟练掌握所涉及的知识点,分类讨论是解题的难点所在.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
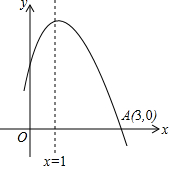 如图是二次函数y=ax2+bx+c图象的一部分,且过点A (3,0),二次函数图象的对称轴是x=1.下列结论:①b2>4ac;②ac>0; ③a-b+c>0; ④4a+2b+c<0.其中错误的结论有( )
如图是二次函数y=ax2+bx+c图象的一部分,且过点A (3,0),二次函数图象的对称轴是x=1.下列结论:①b2>4ac;②ac>0; ③a-b+c>0; ④4a+2b+c<0.其中错误的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>0,?△>0 | B. | a>0,?△<0 | C. | a<0,?△>0 | D. | a<0,?△<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com