已知:抛物线与x轴交于A(-2,0)、B(4,0),与y轴交于C(0,4).
(1)求抛物线顶点D的坐标;
(2)设直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴上下平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可以平移多少个单位长度,向下最多可以平移多少个单位长度?
分析:(1)先设出过A(-2,0)、B(4,0)两点的抛物线的解析式为y=a(x+2)(x-4),再根据抛物线与y轴的交点坐标即可求出a的值,进而得出此抛物线的解析式;
(2)先用待定系数法求出直线CD解析式,再根据抛物线平移的法则得到(1)中抛物线向下平移m各单位所得抛物线的解析式,再将此解析式与直线CD的解析式联立,根据两函数图象有交点即可求出m的取值范围,进而可得到抛物线向下最多可平移多少个单位;同理可求出抛物线向上最多可平移多少个单位.
解答:解:(1)设抛物线解析式为y=a(x+2)(x-4),
∵C点坐标为(0,4),
∴a=-
,(1分)
∴解析式为y=-
x
2+x+4,
顶点D坐标为(1,
);(2分)
(2)直线CD解析式为y=kx+b.
则,
,
∴
,
∴直线CD解析式为y=
x+4,(3分)
∴E(-8,0),F(4,6),
若抛物线向下移m个单位,其解析式y=-
x
2+x+4-m(m>0),
由
消去y,得-
x
2+
x-m=0,
∵△=
-2m≥0,
∴0<m≤
,
∴向下最多可平移
个单位.(5分)
若抛物线向上移m个单位,其解析式y=-
x
2+x+4+m(m>0),
方法一:当x=-8时,y=-36+m,
当x=4时,y=m,
要使抛物线与EF有公共点,则-36+m≤0或m≤6,
∴0<m≤36;(7分)
方法二:当平移后的抛物线过点E(-8,0)时,解得m=36,
当平移后的抛物线过点F(4,6)时,m=6,
由题意知:抛物线向上最多可以平移36个单位长度,(7分)
综上,要使抛物线与EF有公共点,向上最多可平移36个单位,向下最多可平移
个单位.
点评:本题考查的是二次函数的图象与几何变换,涉及到用待定系数法求一次函数与二次函数的解析式、二次函数与一次函数的交点问题,有一定的难度.



 抛物线y=ax2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C,
抛物线y=ax2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C, 与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是
与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是 ,连结AC.
,连结AC.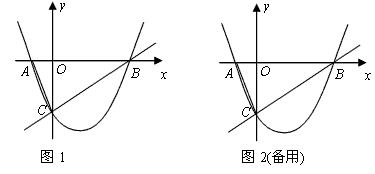
 的顶点坐标是
的顶点坐标是 ]
] 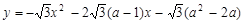 与x轴交于
与x轴交于