
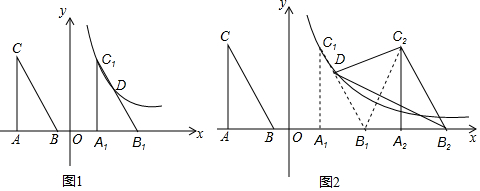
分析 (1)由AB的坐标可求出AB的长度,由CA⊥AB、tan∠ABC=$\frac{4}{3}$,可求出AC的长度,再根据反比例函数图象上点的坐标特征可求出k值,将y=4代入双曲线解析式中可求出点C1的坐标,结合点C的坐标,即可得出△ABC平移的距离;
(2)连接B1C2,根据平行线的性质可得出${S}_{△{B}_{2}{C}_{2}D}$=${S}_{△{B}_{2}{C}_{2}{B}_{1}}$=2S△ABC,进而可得出点B1、B2的坐标,此题得解.
解答 解:(1)∵A(-4,0)、B(-1,0),
∴AB=-1-(-4)=3.
∵CA⊥AB,tan∠ABC=$\frac{4}{3}$,
∴AC=$\frac{4}{3}$AB=4,
∴点C的坐标为(-4,4).
∵点D(3,$\frac{8}{3}$)在双曲线y=$\frac{k}{x}$上,
∴k=3×$\frac{8}{3}$=8,
∴双曲线的解析式为y=$\frac{8}{x}$.
当y=$\frac{8}{x}$=4时,x=2,
∴点C1的坐标为(2,4),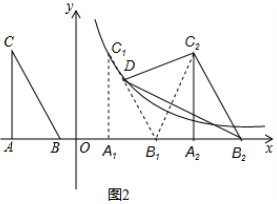
∴△ABC平移的距离为2-(-4)=6.
(2)连接B1C2,如图2所示.
∵△A1B1C1继续向右平移后得△A2B2C2,
∴B1C1∥B2C2,
∴${S}_{△{B}_{2}{C}_{2}D}$=${S}_{△{B}_{2}{C}_{2}{B}_{1}}$=2S△ABC,
∴$\frac{{B}_{1}{B}_{2}•{A}_{2}{C}_{2}}{2}$=2×$\frac{AB•AC}{2}$,
∴B1B2=2AB=6.
∵B(-1,0)且CC1=BB1=6,
∴B1的坐标为(5,0),
∴B2的坐标为(11,0).
点评 本题考查了反比例函数图象上点的坐标特征、坐标与图形变化中的平移、平行线的性质以及解直角三角形,解题的关键是:(1)通过解直角三角形以及反比例函数图象上点的坐标特征求出点C、C1的坐标;(2)根据平行线的性质找出${S}_{△{B}_{2}{C}_{2}D}$=${S}_{△{B}_{2}{C}_{2}{B}_{1}}$=2S△ABC.


科目:初中数学 来源:2017届辽宁省九年级3月月考数学试卷(解析版) 题型:单选题
如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
A. 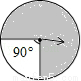 B.
B. 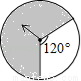 C.
C. 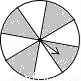 D.
D. 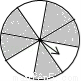
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
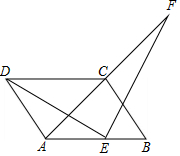 如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com