
【题目】李华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15![]() .(sin15°=0.259,cos15°=0.966,tan15°=0.268,结果精确到0.1m)
.(sin15°=0.259,cos15°=0.966,tan15°=0.268,结果精确到0.1m)
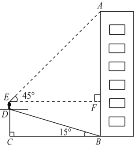
(1)求李华此时与地面的垂直距离CD的值;
(2)李华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45![]() ,求楼房AB的高度.
,求楼房AB的高度.
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
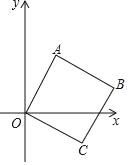
A. (![]() ,-1) B. (2,﹣1) C. (1,-
,-1) B. (2,﹣1) C. (1,-![]() ) D. (﹣1,
) D. (﹣1,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示,则下列结论错误的是( )
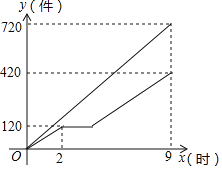
A.甲车间每小时加工服装80件
B.这批服装的总件数为1140件
C.乙车间每小时加工服装为60件
D.乙车间维修设备用了4小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
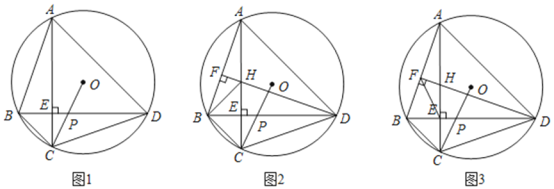
(1)如图1,求证:![]() ;
;
(2)如图2,作![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 长.
长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与计算,请阅读以下材料,并完成相应的问题.
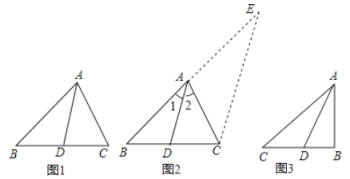
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则![]() =
=![]() .下面是这个定理的部分证明过程.
.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
(1)求代数式m2+m+4的最小值;
(2)求代数式4﹣x2+2x的最大值;
(3)某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
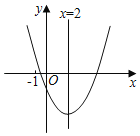
【题目】如图,是二次函数y=ax2+bx+c(a≠0)的图象,对称轴为直线x=2,则下列结论正确的有( )个.
①ax2+bx+c=0(a≠0)有两个不相等的实数根
②3a﹣c>0
③a﹣b+c<0
④(0,y1)、(4,y2)在此二次函数的图象上,则y1<y2
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,销售这种童装每月可获利1800元?
(3)当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com