
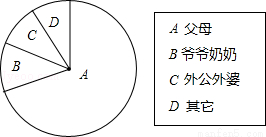
某市在2013年义务教育质量监测过程中,为了解学生的家庭教育情况,就八年级学生平时主要和谁在一起生活进行了抽样调查.下面是根据这次调查情况制作的不完整的频数分布表和扇形统计图.
频数分布表
代码和谁一起生活频数频率
A父母42000.7
B爷爷奶奶660a
C外公外婆6000.1
D其它b0.09
合计60001
请根据上述信息,回答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,和外公外婆一起生活的学生所对应扇形圆心角的度数是 ;
(3)若该市八年级学生共有3万人,估计不与父母一起生活的学生有 人.
(1)0.11;540;(2)36°;(3)9000.
【解析】
试题分析:(1)由表格中的总计减去其它的数字,即可求出a与b的值;
(2)由和外公外婆一起生活的学生的频率为0.1,乘以360度即可得到结果;
(3)求出不与父母一起生活学生的频率,乘以30000即可得到结果.
试题解析:(1)根据表格得:a=1-(0.7+0.1+0.09)=0.11,b=6000-(4200+660+600)=540;
(2)根据题意得:和外公外婆一起生活的学生所对应扇形圆心角的度数是360°×0.1=36°;
(3)根据题意得:30000×(1-0.7)=9000(人),
则估计不与父母一起生活的学生有9000人.
考点:频数(率)分布表;用样本估计总体;扇形统计图.


科目:初中数学 来源:2013-2014学年北京市大兴区中考一模数学试卷(解析版) 题型:解答题
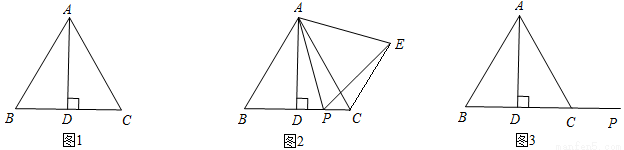
在等边三角形ABC中,AD⊥BC于点D.
(1)如图1,请你直接写出线段AD与BC之间的数量关系: AD= BC ;
(2)如图2,若P是线段BC上一个动点(点P不与点B、C重合),联结AP,将线段AP绕点A逆时针旋转60°,得到线段AE,联结CE,猜想线段AD、CE、PC之间的数量关系,并证明你的结论;
(3)如图3,若点P是线段BC延长线上一个动点,(2)中的其他条件不变,按照(2)中的作法,请在图3中补全图形,并直接写出线段AD、CE、PC之间的数量关系.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市大兴区中考一模数学试卷(解析版) 题型:选择题
已知:如图,PA切⊙O于点A,PB切⊙O于点B,如果∠APB=60°,⊙O半径是3,则劣弧AB的长为( )
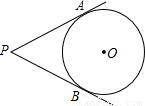
A.π B.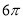 C.2π D.3π
C.2π D.3π
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市丰台区中考二模数学卷(解析版) 题型:解答题
如图,经过原点的抛物线y=-x2+bx(b>2)与x轴的另一交点为A,过点P(1,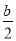 )作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.
)作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.
(1)当b=4时,求点A的坐标及BC的长;
(2)连结CA,求b的适当的值,使得CA⊥CP;
(3)当b=6时,如图2,将△CBP绕着点C按逆时针方向旋转,得到△CB′P′,CP与抛物线对称轴的交点为E,点M为线段B′P′(包含端点)上任意一点,请直接写出线段EM长度的取值范围.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市丰台区中考二模数学卷(解析版) 题型:选择题
如图,正方形ABCD的边长为2cm,在对称中心O处有一个钉子.动点P、Q同时从点A出发,点P沿A-B-C方向以每秒2cm的速度运动,到C点停止,点Q沿A-D方向以每秒1cm的速度运动,到D点停止.PQ两点用一条可伸缩的细橡皮筋联结,当遇到钉子后,橡皮筋会自动弯折.如果x秒后橡皮筋扫过的面积为ycm2,那么y与x的函数关系图象可能是( )

A.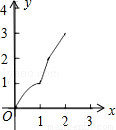 B.
B.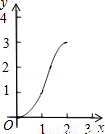 C.
C.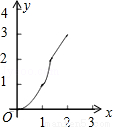 D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古满洲里市九年级三月月考数学试卷(解析版) 题型:填空题
在实数的原有运算法则中我们补充定义新运算“⊕”如下:当a≥b时,a⊕b=b2;当a<b时,a⊕b=a. 则当x=2时,(1⊕x)-(3⊕x)的值为 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古呼伦贝尔市九年级第四次月考数学试卷(解析版) 题型:解答题
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,其中A点坐标为(-1,0), 点C(0,5),点D(1,8)在抛物线上,M为抛物线的顶点.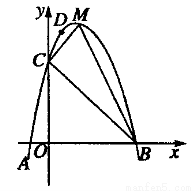 求
求
(1)抛物线的解析式;
(2)求△MCB的面积.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com