练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．有一批铅笔分给几个小朋友，若每个小朋友分5支，则还余2支；每个小朋友分6支，那么最后一个小朋友分到了铅笔，但少于2支，求小朋友人数和铅笔支数．

    分析 设小朋友的人数为x，根据“每个小朋友分5支，还余2支”可知铅笔总数为（5x+2）支，再根据“若每个小朋友分6支，那么最后一个小朋友分得的铅笔少于2支”，列出不等式组，求出解集，由此分别解出小朋友人数和铅笔支数．

    解答 解：设小朋友人数为x，则铅笔支数为（5x+2）支．
    由题意，有0≤（5x+2）-6（x-1）＜2，
    解得6＜x≤8．
    ∵x为整数，
    ∴x=7或8．
    当x=7时，5x+2=37；
    当x=8时，5x+2=42．
    答：小朋友人数为7时，铅笔支数是为37；小朋友人数为8时，铅笔支数为42支．

    点评 考查了一元一次不等式组的应用，本题主要是根据“若每个小朋友分6支，那么最后一个小朋友分得的铅笔少于2支”，列出不等式组．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    19．如图为张小亮的答卷，他的得分应是（　　）
    A．100分B．80分C．60分D．40分

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如图所示的圆锥的主视图是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，将一张四边形纸片沿直线剪开，如果剪开后的两个图形的内角和相等，下列四种剪法中，符合要求的是（　　）
    A．①②B．①③C．②④D．③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

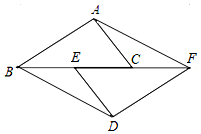    4．如图，点B、E、C、F在一条直线上，AB=DF，AC=DE，BE=FC．
    （1）求证：△ABC≌△DFE；
    （2）连接AF、BD，求证：四边形ABDF是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

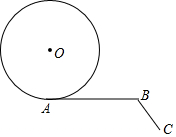    7．如图，已知∠ABC=120°，AB=πr，BC=$\frac{πr}{2}$，半径为r的⊙O从点A出发，沿A→B→C方向滚动到点C时停止，则圆心O运动的路程是$\frac{11}{6}$πr．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．化简$\frac{a}{a-b}$-$\frac{b}{a+b}$的结果是（　　）
    A．$\frac{{a}^{2}{+b}^{2}}{{a}^{2}{-b}^{2}}$B．$\frac{{（a+b）}^{2}}{{a}^{2}{-b}^{2}}$C．$\frac{{a}^{2}{-b}^{2}}{{a}^{2}{+b}^{2}}$D．$\frac{{a}^{2}{+b}^{2}}{{（a-b）}^{2}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．解不等式组：$\left\{\begin{array}{l}{4（x-1）＜3x-4（1）}\\{\frac{1+2x}{3}＞x-1（2）}\end{array}\right.$
    请结合题意填空：完成本题的解答：
    （Ⅰ）解不等式（1），得x＜0；
    （Ⅱ）解不等式（2），得x＜4；
    （Ⅲ）把不等式（1）和（2）的解集在数轴上表示出来：

    （Ⅳ）原不等式组的解集为x＜0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．人民商场销售某种冰箱，每台进价为2500元，市场调研表明：当每台销售价定为2900元时，平均每天能售出8台；每台售价每降低50元，平均每天能多售出4台．
    设该种冰箱每台的销售价降低了x元．
    （1）填表：
    每天售出的冰箱台数（台）每台冰箱的利润（元）
    降价前8400
    降价后8+$\frac{x}{50}$×4400-x
    （2）若商场要想使这种冰箱的销售利润平均每天达到5000元，则每台冰箱的售价应定为多少元？

    查看答案和解析>>

    同步练习册答案