
分析 首先根据1*2=-9,(-3)*3=-2,可得$\left\{\begin{array}{l}{a+2b-5=-9}\\{-3a+3b-5=-2}\end{array}\right.$,据此求出a、b的值各是多少;然后应用代入法,求出2a-b的值是多少即可.
解答 解:∵1*2=-9,(-3)*3=-2,
∴$\left\{\begin{array}{l}{a+2b-5=-9①}\\{-3a+3b-5=-2②}\end{array}\right.$
①×3+②,可得:9b-20=-29
解得b=-1,
把b=-1代入①,解得a=-2,
∴2a-b=2×(-2)-(-1)=-3.
故答案为:-3.
点评 此题主要考查了解二元一次方程的方法和应用,以及有理数的混合运算的运算方法,要熟练掌握,注意加减法在解二元一次方程组中的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,春节来临,小明约同学周末去文化广场放风筝,他放的风筝线AE长为115m,他的风筝线(近似地看作直线)与水平地面构成42°角,若小明身高AB为1.42m,求他的风筝飞的高度CF(精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
如图,春节来临,小明约同学周末去文化广场放风筝,他放的风筝线AE长为115m,他的风筝线(近似地看作直线)与水平地面构成42°角,若小明身高AB为1.42m,求他的风筝飞的高度CF(精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
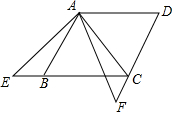 如图,四边形ABCD是菱形,AB=4,∠ABC=60°,E,F分别在CB,DC的延长线上,且∠EAF=60°,∠EAB=15°,则S△ACF=6-2$\sqrt{3}$.
如图,四边形ABCD是菱形,AB=4,∠ABC=60°,E,F分别在CB,DC的延长线上,且∠EAF=60°,∠EAB=15°,则S△ACF=6-2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点之间的距离就是两点间的线段 | |
| B. | 与同一条直线垂直的两条直线也垂直 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 过一点有且只有一条直线与已知直线垂直 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com