练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
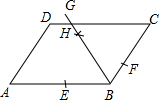
    13．如图，在?ABCD中，AB＞2BC，观察图中尺规作图的痕迹，则下列结论错误的是（　　）
    A．BG平分∠ABCB．BE=BFC．AD=CHD．CH=DH

    分析 根据角平分线的性质与平行四边形的性质对各选项进行逐一分析即可．

    解答 解：A、由作法可知BG平分∠ABC，故本选项不符合题意；
    B、由作法可知BE=BF，故本选项不符合题意；
    C、过点H作HM∥AD，可得四边形BCHM是菱形，所以AD=CH，故本选项不符合题意；
    D、由于AB＞2BC，所以CH∥DH，故本选项符合题意．
    故选D．

    点评 本题考查的是作图-基本作图，熟知角平分线的作法是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

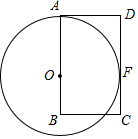    3．如图，矩形ABCD中，AB=9，O是AB边上一点，以O为圆心，OA为半径画圆与边CD相切于点F，与BC相交于点E，若EC=2，则⊙O的半径为5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

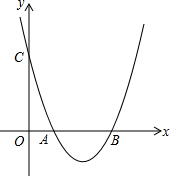    4．已知二次函数y=a（x-1）（x-3）（a＞0）的图象与x轴交于A、B两点（A左B右），与y轴交于C点（0，3）．P为x轴下方二次函数y=a（x-1）（x-3）（a＞0）图象上一点，P点横坐标为m．
    （1）求a的值；
    （2）若P为二次函数y=a（x-1）（x-3）（a＞0）图象的顶点，求证：∠ACO=∠PCB；
    （3）Q（m+n，y0）为二次函数y=a（x-1）（x-3）（a＞0）图象上一点，且∠ACO=∠QCB，求n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：
    （1）$\sqrt{8}$+|1-$\sqrt{2}$|-π0+${（\frac{1}{2}）}^{-1}$  
    （2）（$\sqrt{8}$+$\sqrt{3}$）×$\sqrt{6}$-（4$\sqrt{2}$-3$\sqrt{6}$）÷2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：
    （1）$\sqrt{0.04}$+$\root{3}{-27}$+$\sqrt{{（-3）}^{2}}$-（-1）2017
    （2）$\sqrt{16}$-$\root{3}{64}$-$\sqrt{{（-5）}^{2}}$-|$\sqrt{3}$-2|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=130°，则∠F等于（　　）
    A．9.5°B．19°C．15°D．30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．【阅读理解】我们知道，当a＞0且b＞0时，（$\sqrt{a}$-$\sqrt{b}$）2≥0，所以a-2$\sqrt{ab}$+≥0，从而a+b≥2$\sqrt{ab}$（当a=b时取等号），
    【获得结论】设函数y=x+$\frac{a}{x}$（a＞0，x＞0），由上述结论可知：当x=$\frac{a}{x}$即x=$\sqrt{a}$时，函数y有最小值为2$\sqrt{a}$
    【直接应用】（1）若y1=x（x＞0）与y2=$\frac{1}{x}$（x＞0），则当x=1时，y1+y2取得最小值为2．
    【变形应用】（2）若y1=x+1（x＞-1）与y2=（x+1）2+4（x＞-1），则$\frac{{y}_{2}}{{y}_{1}}$的最小值是4
    【探索应用】（3）在平面直角坐标系中，点A（-3，0），点B（0，-2），点P是函数y=$\frac{6}{x}$在第一象限内图象上的一个动点，过P点作PC⊥x轴于点C，PD⊥y轴于点D，设点P的横坐标为x，四边形ABCD的面积为S
    ①求S与x之间的函数关系式；
    ②求S的最小值，判断取得最小值时的四边形ABCD的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在平面直角坐标系xOy中，已知正比例函数的图象与反比例函数y=$\frac{8}{x}$的图象交于点A（m，4）．
    （1）求正比例函数的解析式；
    （2）将正比例函数的图象向下平移6个单位得到直线l，设直线l与x轴的交点为B，求∠ABO的正弦值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知a，b都是实数，且（12a+b）2+|3a-b-5|=0，求13a2-b的平方根．

    查看答案和解析>>

    同步练习册答案