
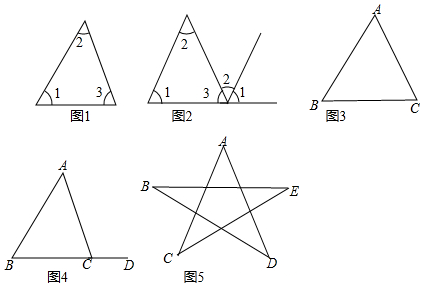
分析 (1)过点C作CM∥AB,根据平行线的性质、平角的定义证明;
(2)①根据三角形内角和定理和平角的定义解答;
②根据三角形的外角的性质、三角形内角和定理计算即可.
解答 证明:(1)如图3,过点C作CM∥AB,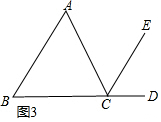 ∴∠ECD=∠B,∠ECA=∠A,
∴∠ECD=∠B,∠ECA=∠A,
∵∠BCA+∠ECA+∠ECD=180°,
∴∠BCA+∠A+∠B=180°;
(2)解:①∵∠BCA+∠A+∠B=180°,∠BCA+∠ACD=180°
∴∠ACD=∠A+∠B,
故答案为:∠A+∠B;
②对于△BDN,∠MNA=∠B+∠D,
对于△CEM,∠NMA=∠C+∠E,
对于△ANM,∠A+∠MNA+∠NMA=180°,
∴∠A+∠B+∠D+∠C+∠E=180°.
点评 本题考查的是三角形内角和定理的应用、三角形的外角的性质,掌握三角形内角和等于180°、三角形的一个外角等于与它不相邻的两个内角之和是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
| 单价(元) | 50 | 40 | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
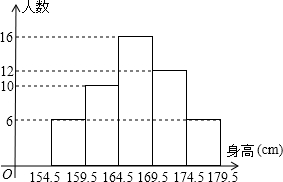 为了了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得打的数据(身高取整数)整理后,画出频数分布直方图(如图所示),图中从左到右依次为第1,2,3,4,5组.
为了了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得打的数据(身高取整数)整理后,画出频数分布直方图(如图所示),图中从左到右依次为第1,2,3,4,5组.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com