
����Ŀ����ͼ���߳�Ϊ1��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����ֱ�ǡ�MPN��ʹֱ�Ƕ���P���O�غϣ�ֱ�DZ�PM��PN�ֱ���OA��OB�غϣ�Ȼ����ʱ����ת��MPN����ת��Ϊ�ȣ�0�㣼�ȣ�90�㣩��PM��PN�ֱ�AB��BC��E��F���㣬����EF��OB�ڵ�G�������н�������ȷ���� ��
��1��EF=![]() OE����2��S�ı���OEBF��S������ABCD=1��4����3��BE+BF=
OE����2��S�ı���OEBF��S������ABCD=1��4����3��BE+BF=![]() OA����4������ת�����У�����BEF����COF�����֮�����ʱ��AE=
OA����4������ת�����У�����BEF����COF�����֮�����ʱ��AE=![]() ����5��OGBD=AE2+CF2��
����5��OGBD=AE2+CF2��
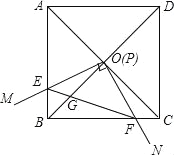
���𰸡���1������2������3������5����
��������
�����������1�����ı���ABCD�������Σ�
��OB=OC����OBE=��OCF=45�㣬��BOC=90�㣬
���BOF+��COF=90�㣬
�ߡ�EOF=90�㣬
���BOF+��COE=90�㣬
���BOE=��COF��
�ڡ�BOE�͡�COF�У�
 ��
��
���BOE�ա�COF��ASA����
��OE=OF��BE=CF��
��EF=![]() OE������ȷ��
OE������ȷ��
��2����S�ı���OEBF=S��BOE+S��BOE=S��BOE+S��COF=S��BOC=![]() S������ABCD��
S������ABCD��
��S�ı���OEBF��S������ABCD=1��4������ȷ��
��3����BE+BF=BF+CF=BC=![]() OA������ȷ��
OA������ȷ��
��4������O��OH��BC��
��BC=1��
��OH=![]() BC=
BC=![]() ��
��
��AE=x����BE=CF=1��x��BF=x��
��S��BEF+S��COF=![]() BEBF+
BEBF+![]() CFOH=
CFOH=![]() x��1��x��+
x��1��x��+![]() ��1��x����
��1��x����![]() =��
=��![]() ��x��
��x��![]() ��2+
��2+![]() ��
��
��a=��![]() ��0��
��0��
�൱x=![]() ʱ��S��BEF+S��COF���
ʱ��S��BEF+S��COF���
������ת�����У�����BEF���COF�����֮�����ʱ��AE=![]() ���ʴ���
���ʴ���
��5���ߡ�EOG=��BOE����OEG=��OBE=45�㣬
���OEG�ס�OBE��
��OE��OB=OG��OE��
��OGOB=OE2��
��OB=![]() BD��OE=
BD��OE=![]() EF��
EF��
��OGBD=EF2��
���ڡ�BEF�У�EF2=BE2+BF2��
��EF2=AE2+CF2��
��OGBD=AE2+CF2������ȷ��



 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д� Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����M����2��1������y��ĶԳƵ�N�������ǣ�������
A. ��2��1�� B. ��1����2�� C. ����2����1�� D. ��2����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2y��7x��0����x��y����( )
A. 7��2 B. 4��7 C. 2��7 D. 7��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��a+4����5��b�����Q��2b��2a+8������ԭ������ĶԳƣ�a+b2 =___.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.�Ȼ����Ե�Բ�Ľ����B.�Ż�һ�������ӻ�
C.�������������һ��ԲD.��ȵ�Բ�Ľ����ԵĻ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У�����D��DE��AB�ڵ�E����F �ڱ�CD�ϣ�DF=BE������AF��BF�� 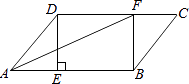
��1����֤���ı���BFDE�Ǿ��Σ�
��2����CF=3��BF=4��DF=5����֤��AFƽ�֡�DAB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
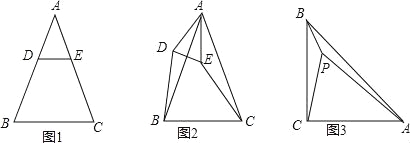
����Ŀ����֪��ABC�ǵ��������Σ�AB=AC��
��1���������Σ���ͼ1����DE��BCʱ����DB EC�������������������=����
��2������̽��������ͼ1�е���ADE�Ƶ�A˳ʱ����ת����0�㣼����180�㣩��ͼ2λ�ã���1���еĽ��ۻ��������������������֤����������������˵�����ɣ�
��3����չ���ã���ͼ3��P�ǵ���ֱ��������ABC��һ�㣬��ACB=90�㣬��PB=1��PC=2��PA=3������BPC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
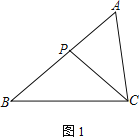
����Ŀ������ABC�У�PΪ��AB��һ����
(1) ��ͼ1������ACP����B����֤��AC2��AP��AB��
(2) ��MΪCP���е㣬AC��2��
�� ��ͼ2������PBM����ACP��AB��3����BP�ij���
�� ��ͼ3������ABC��45������A����BMP��60����ֱ��д��BP�ij���
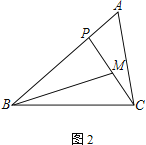
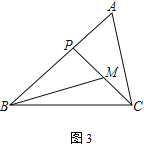
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com