
ij������Ʒ�̵�����һ��ɱ�Ϊ50Ԫ�����涨�����ڼ䵥�۲����ڳɱ��ۣ��һ������ø���40%�����������֣�������y�����������۵���x��Ԫ��֮��������ͼ��ʾ��һ�κ�����ϵ��
��1����ȷ��y��x֮��ĺ�����ϵʽ��
��2������������Ʒ�̵������������������õ�����QԪ����д������Q��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ�����������۶�Ϊ����Ԫʱ�����̵�ɻ����������������Ƕ���Ԫ��
��3�������̵����������������õ�������600Ԫ����ȷ�����۵���x��ȡֵ��Χ��
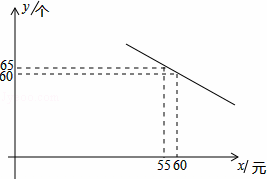


�⣺��1����y=kx+b����������ý�ã�
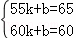
k=��1��b=120��
����һ�κ����ı���ʽΪy=��x+120��
��2������W�����۵���x֮��ĺ�����ϵʽΪ��Q=��x��50������x+120��=��x2+170x��6000��
Q=��x2+170x��6000=����x��85��2+1225��
���Ե��������۶�Ϊ85Ԫʱ�����̵�ɻ�����������������1225Ԫ��
��3����600=��x2+170x��6000��
��ã�x1=60��x2=90��
�������ø���40%��
����۸�Ϊ50��1+50%��=75��
��60��x��75��������
�ʴ�Ϊ��60��x��75��������





| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ1����ƽ��ƽ��״̬����������������һ���������Ҳ������Ҳ��һ����������2����20�˵����룮�ֽ�������һ�Ų����������Ҳ���̣��������Ҳ���̵�1���������ƽ�Գ�ƽ��״̬����ͼ2�����ƶ��IJ����������Ϊ��������
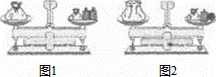
�� A�� 10�� B�� 15�� C�� 20�� D�� 25��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��2014��������籭������ǰϦ��ij������Ʒ�깺��һ������Ϊ40Ԫ����������������60Ԫ���ۣ���ôһ�����ڿ��۳�240��.�������۾��飬������۵��ۻᵼ���������ļ��٣������۵���ÿ���5Ԫ����������Ӧ����20��.�����۵���Ϊx��x��60��Ԫ��������Ϊy��.
��1�����y��x�ĺ�����ϵʽ.
��2�������۵���Ϊ����Ԫʱ�������۶�Ϊ14 000Ԫ��
000Ԫ��
 ��3�������۵���Ϊ��
��3�������۵���Ϊ�� ��Ԫʱ��������һ�����ڻ�����������������Ƕ��٣�
��Ԫʱ��������һ�����ڻ�����������������Ƕ��٣�
[�ο���ʽ��������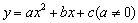 �Ķ��������� ]
�Ķ��������� ]


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���۵�����ABCD��һ��AD��ʹ��D����BC�ߵĵ�F������֪AB=8cm��BC=10cm����tan��EAF��ֵ=������



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����֪��O��ֱ��AB����AC�ļн�Ϊ30�㣬����C����O�����߽�AB���ӳ����ڵ�D��OD=30cm����ֱ��AB�ij���
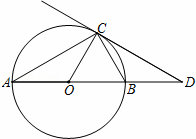


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��һ����ֵ100Ԫ������ң��һ���10Ԫ��20Ԫ����Ǯ���һ������� ( )
A��6�� B��7�� C��8�� D��9��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���������չ����������ʾ. 2014�����뱾�������������Ѳ�������Ԥ���ȥ�����Ԥ�����8.18��Ԫ.�ÿ�ѧ��������ʾΪ8.18��Ԫ_______________Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
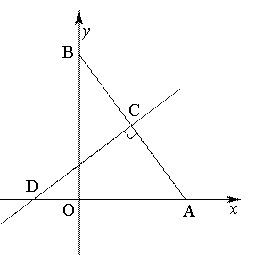
��ͼ����ƽ��ֱ������ϵ�У���֪Rt��AOB����ֱ�DZ�OA��OB�ֱ���x�ᡢy����������ϣ�OA<OB������OA��OB�ij��ֱ���һԪ���η���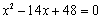 ��������.�߶�AB�Ĵ�ֱƽ����CD��AB�ڵ�C����x���ڵ�D.��P��ֱ��CD�ϵ�һ�����㣬��Q��ֱ��AB�ϵ�һ������.
��������.�߶�AB�Ĵ�ֱƽ����CD��AB�ڵ�C����x���ڵ�D.��P��ֱ��CD�ϵ�һ�����㣬��Q��ֱ��AB�ϵ�һ������.
��1����A��B��������ꣻ
��2����ֱ��CD�Ľ���ʽ��
��3��������ƽ�����Ƿ���ڵ�M��ʹ�Ե�C��P��Q��MΪ������ı����������Σ��Ҹ������εı߳�Ϊ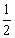 AB��.�����ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
AB��.�����ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��a=192��918��b=8882��302��c=10532��7472������a��b��c����С�����˳�����У�������� ����������������


�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com