
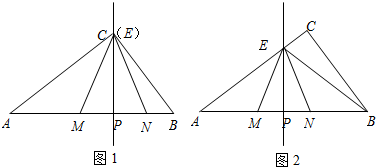
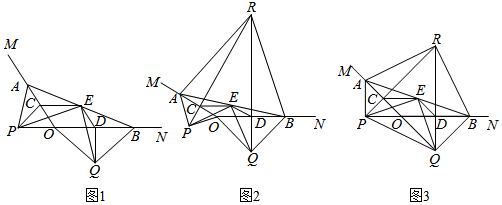
分析 ((1)本题需先根据已知条件得出AC的值,再根据CP⊥AB求出CP,从而得出CM的值.
(2)本题需先根据EN,根据sin∠EMP=$\frac{12}{13}$,设出EP的值,从而得出EM和PM的值,再得出△AEP∽△ABC,即可求出$\frac{PE}{AP}$=$\frac{BC}{AC}$,求出a的值,即可得出y关于x的函数关系式,并且能求出函数的定义域.
(3)本题需先设EP的值,得出则EM和MP的值,然后分①点E在AC上时,根据△AEP∽△ABC,求出AP的值,从而得出AM和BN的值,再根据△AME∽△ENB,求出a的值,得出AP的长;②点E在BC上时,根据△EBP∽△ABCC,求出AP的值,从而得出AM和BN的值,再根据△AME∽△ENB,求出a的值,得出AP的长.
解答 解:(1)∵∠ACB=90°,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{5{0}^{2}-3{0}^{2}}$=40,
∵CP⊥AB,
∴$\frac{AB•CP}{2}$=$\frac{AC•BC}{2}$,
∴$\frac{30×40}{2}$=$\frac{50•CP}{2}$,
∴CP=24,
∴CM=$\frac{CP}{sin∠EMP}$=$\frac{24}{\frac{12}{13}}$=26;
(2)∵sin∠EMP=$\frac{12}{13}$,
∴设EP=12a,
则EM=13a,PM=5a,
∵EM=EN,
∴EN=13a,PN=5a,
∵△AEP∽△ABC,
∴$\frac{PE}{AP}=\frac{BC}{AC}$,
∴$\frac{12a}{x}$=$\frac{30}{40}$
∴x=16a,
∴a=$\frac{x}{16}$,
∴BP=50-16a,
∴y=50-21a,
=50-21×$\frac{x}{16}$,
=50-$\frac{21}{16}$x,
∵当E点与A点重合时,x=0.当E点与C点重合时,x=32.
∴函数的定义域是:(0<x<32);
(3)
①当点E在AC上时,如图2,设EP=12a,则EM=13a,MP=NP=5a,
∵△AEP∽△ABC,
∴$\frac{AP}{AC}$=$\frac{EP}{BC}$,
∴$\frac{AP}{40}$=$\frac{12a}{30}$,
∴AP=16a,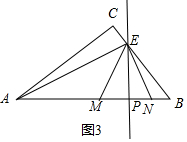
∴AM=11a,
∴BN=50-16a-5a=50-21a,
∵△AME∽△ENB,
∴$\frac{AM}{EN}$=$\frac{EM}{NB}$
∴$\frac{11a}{13a}$=$\frac{13a}{50-21a}$,
∴a=$\frac{11}{8}$,
∴AP=16×$\frac{11}{8}$=22,
②当点E在BC上时,如图(备用图),设EP=12a,则EM=13a,MP=NP=5a,
∵△EBP∽△ABC,
∴$\frac{BP}{BC}$=$\frac{EP}{AC}$,
即$\frac{BP}{30}$=$\frac{12a}{40}$,
解得BP=9a,
∴BN=9a-5a=4a,AM=50-9a-5a=50-14a,
∵△AME∽△ENB,
∴$\frac{AM}{EN}$=$\frac{ME}{BN}$,
即$\frac{50-14a}{13a}$=$\frac{13a}{4a}$,
解得a=$\frac{8}{9}$,
∴AP=50-9a=50-9×$\frac{8}{9}$=42.
所以AP的长为:22或42.
点评 本题主要考查了相似三角形的判定和性质、勾股定理、解直角三角形,在解题时要注意知识的综合应是解本题的关键.


科目:初中数学 来源: 题型:解答题
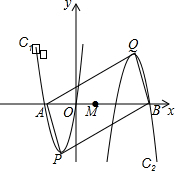 如图,抛物线C1:y1=ax2+2ax(a>0)与x轴交于点A,顶点为点P.
如图,抛物线C1:y1=ax2+2ax(a>0)与x轴交于点A,顶点为点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
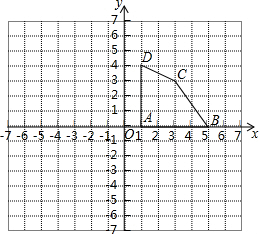 如图,四边形ABCD各顶点的坐标分别为A(1,0),B(5,0),C(3,3),D(1,4).将四边形ABCD先向下平移4个单位长度,再向左平移6个单位长度,得到四边形A′B′C′D′.
如图,四边形ABCD各顶点的坐标分别为A(1,0),B(5,0),C(3,3),D(1,4).将四边形ABCD先向下平移4个单位长度,再向左平移6个单位长度,得到四边形A′B′C′D′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com