
【题目】如图,一次函数y=kx+2的图象与反比例函数y=![]() 的图象交于A、B两点,其中A点坐标为(2,3).
的图象交于A、B两点,其中A点坐标为(2,3).
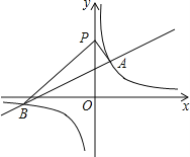
(1)求两个函数的表达式;
(2)点P是y轴上的一个动点,当∠APB为直角时,求P点坐标.
【答案】(1)y=![]() x+2, y=
x+2, y=![]() ;(2)P(0,5)或(0,-3).
;(2)P(0,5)或(0,-3).
【解析】
(1)根据待定系数法,即可求解;
(2)先算出B(-6,-1),作AM⊥y轴于M,BN⊥y轴于N,设P(0,n),易得△APM∽△PBN,进而得![]() =
=![]() ,即可求解.
,即可求解.
(1)∵A(2,3)为一次函数与反比例函数图象的交点,
∴将A(2,3)代入一次函数解析式得:3=2k+2,
解得:k=![]() ,
,
将A(2,3)代入反比例函数解析式得:3=![]() ,
,
解得:a=6,
∴一次函数的解析式为y=![]() x+2,反比例函数的表达式为y=
x+2,反比例函数的表达式为y=![]() ;
;
(2)联立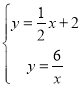 ,解得:
,解得:![]() 或
或![]() ,
,
∴B(-6,-1),
作AM⊥y轴于M,BN⊥y轴于N,设P(0,n),
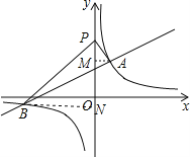
∴M(0,3),N(0,-1),
∴AM=2,BN=6,PM=|n-3|,PN=|n+1|
∵∠APB为直角,
∴∠BPN+∠APM=∠APM+∠PAM,
∴∠BPN=∠PAM,
∵∠PNB=∠AMP=90°,
∴△APM∽△PBN,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:n=5或n=-3,
∴P(0,5)或(0,-3).


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
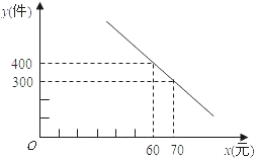
【题目】某服装公司试销一种成本为每件50元的T恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
(1)求y与x之间的函数关系式;
(2)设公司获得的总利润(总利润=总销售额-总成本)为P元,求P与x之间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数经过点B(3,0),C(0,3),D(4,-5)
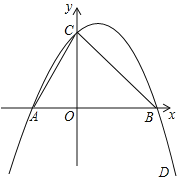
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)若P是抛物线上一点,且S△ABP=![]() S△ABC,这样的点P有几个请直接写出它们的坐标.
S△ABC,这样的点P有几个请直接写出它们的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
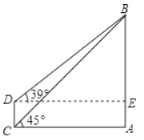
【题目】目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从-3、-1、![]() 、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=-x+a的图象与坐标轴围成三角形的面积不超过4的概率为______.
、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=-x+a的图象与坐标轴围成三角形的面积不超过4的概率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为_____.
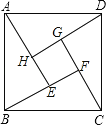
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com