
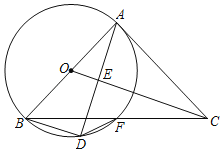
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,以AB为直径的⊙O交BC于点F,连结OC,过点B作BD∥OC交⊙O点D.连接AD交OC于点E
(1)求证:BD=AE.
(2)若OE=1,求DF的值.
【答案】(1)见解析;(2)DF=![]()
【解析】
(1)由余角的性质可证∠BAD=∠ACE,然后根据“AAS”证明△ADB≌△CEA,即可解决问题.
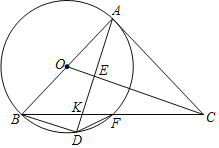
(2)由三角形的中位线可求BD的长,根据全等三角形的性质和垂径定理可求出AE、DE的长,根据勾股定理求出AB的长,根据平行线分线段成比例求出DK,进而求出BK,然后通过证明△AKB∽△FKD,利用相似三角形的性质求解即可解决问题.
(1)证明:∵AB是直径,
∴∠ADB=90°,
∵BD∥OC,
∴∠AEO=∠ADB=90°,
∵∠OAC=90°,
∴∠OAE+∠AOC=90°,∠AOC+∠ACO=90°,
∴∠BAD=∠ACE,
∵AB=AC,∠ADB=∠AEC=90°,
∴△ADB≌△CEA(AAS),
∴AE=BD.
(2)∵OE∥BD,AO=OB,
∴AE=ED,
∴BD=2OE=2,
∴AE=BD=DE=2,
∴AB=![]() =2
=2![]() ,
,![]()
∵△ADB≌△CEA,
∴EC=AD=4,
设AD交BC于K.
∵EC∥BD,
∴![]() =
=![]() =2,
=2,
∴DK=![]() ,
,
∴BK=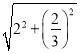 =
=![]() ,
,
∵∠ABK=∠FDK,∠AKB=∠FKD,
∴△AKB∽△FKD,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴DF=![]() .
.


科目:初中数学 来源: 题型:
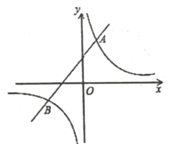
【题目】如图,已知反比例函数![]() 与一次函数
与一次函数![]() 的图象在第一象限相交于点
的图象在第一象限相交于点![]() .
.
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点![]() 的坐标,并根据图像写出使反比例函数的值大于一次函数的值的
的坐标,并根据图像写出使反比例函数的值大于一次函数的值的![]() 取值范围.
取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
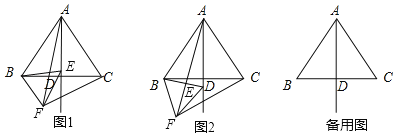
【题目】已知△ABC是等边三角形,AD⊥BC于点D,点E是直线AD上的动点,将BE绕点B顺时针方向旋转60°得到BF,连接EF、CF、AF.
(1)如图1,当点E在线段AD上时,猜想∠AFC和∠FAC的数量关系;(直接写出结果)
(2)如图2,当点E在线段AD的延长线上时,(1)中的结论还成立吗?若成立,请证明你的结论,若不成立,请写出你的结论,并证明你的结论;
(3)点E在直线AD上运动,当△ACF是等腰直角三角形时,请直接写出∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
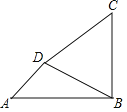
【题目】如图,海中有两个小岛![]() ,
,![]() ,某渔船在海中的
,某渔船在海中的![]() 处测得小岛D位于东北方向上,且相距
处测得小岛D位于东北方向上,且相距![]() ,该渔船自西向东航行一段时间到达点
,该渔船自西向东航行一段时间到达点![]() 处,此时测得小岛
处,此时测得小岛![]() 恰好在点
恰好在点![]() 的正北方向上,且相距
的正北方向上,且相距![]() ,又测得点
,又测得点![]() 与小岛
与小岛![]() 相距
相距![]() .
.
(1)求![]() 的值;
的值;
(2)求小岛![]() ,
,![]() 之间的距离(计算过程中的数据不取近似值).
之间的距离(计算过程中的数据不取近似值).
查看答案和解析>>
科目:初中数学 来源: 题型:
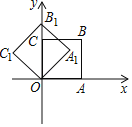
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果按此速度增涨,该公司六月份的快递件数将达到多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
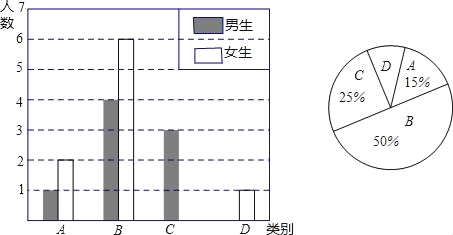
【题目】李老师为了了解班级学生自主学习、合作交流的具体情况,对九(1)班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C;一般;D:较差,并将调查结果绘制成以下两幅不完整的统计图.请你根据统计图解答下列问题:
(1)本次调查中,李老师一共调查了 名同学,其中女生共有 名.
(2)将上面的条形统计图补充完整;
(3)为了共同进步,李老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请求所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE
(Ⅰ)求证:AE是⊙O的切线;
(Ⅱ)若∠DBC=30°,DE=1 cm,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com