
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.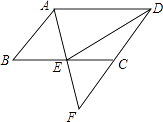
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠ABE=∠FCE,
∵E为BC中点,
∴BE=CE,
在△ABE与△FCE中,
 ,
,
∴△ABE≌△FCE(ASA),
∴AB=FC;
(2)
证明:∵AD=2AB,AB=FC=CD,
∴AD=DF,
∵△ABE≌△FCE,
∴AE=EF,
∴DE⊥AF.
【解析】(1)由在ABCD中,E是BC的中点,利用ASA,即可判定△ABE≌△FCE,继而证得结论;(2)由AD=2AB,AB=FC=CD,可得AD=DF,又由△ABE≌△FCE,可得AE=EF,然后利用三线合一,证得结论.
此题考查了平行四边形的性质、全等三角形的判定与性质以及等腰三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,∠BAD的平分线交BD于点E , 交CD于点F , 交BC的延长线于点G , 则下列结论中正确的是( ) 
A.AE2=EFFG
B.AE2=EFEG
C.AE2=EGFG
D.AE2=EFAG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
根据以上规则,回答下列问题: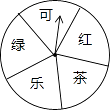
(1)求一次“有效随机转动”可获得“乐”字的概率;
(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或树状图等方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 . (填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈ ![]() ,tan48°≈
,tan48°≈ ![]() ,sin64°≈
,sin64°≈ ![]() ,tan64°≈2)
,tan64°≈2)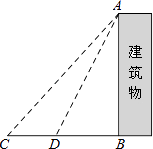
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com