
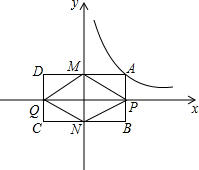
 在平面直角坐标系中,一动点A在双曲线y=$\frac{12}{x}$上(x>0)移动,A点关于x、y轴的对称点分别为点B、D,B点关于y轴的对称点是点C,AB、CD分别交x轴于点P、Q,AD、BC分别交y轴于点M、N.
在平面直角坐标系中,一动点A在双曲线y=$\frac{12}{x}$上(x>0)移动,A点关于x、y轴的对称点分别为点B、D,B点关于y轴的对称点是点C,AB、CD分别交x轴于点P、Q,AD、BC分别交y轴于点M、N.分析 (1)根据轴对称的性质即可得出结论;
(2)根据矩形的性质即可得出结论;
(3)根据点A在反比例函数y=$\frac{12}{x}$上,故可得出矩形的面积是定值,由此可得出结论.
解答 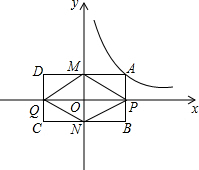 (1)解:∵点A、B关于x轴对称,点A、D关于y轴对称,
(1)解:∵点A、B关于x轴对称,点A、D关于y轴对称,
∴AB⊥AD.
∵点CD关于x轴对称,
∴CD=AB,AD=BC,
∴四边形ABCD是矩形.
故答案为:矩;
(2)解:由(1)知,四边形ABCD是矩形,且点A、B关于x轴对称,点A、D关于y轴对称,
∴AP=BP,DM=AM,
∴PM=MQ.
同理PM=MQ=QN=PN,
∴四边形PMQN是菱形;
(3)∵点A在双曲线y=$\frac{12}{x}$上(x>0),
∴矩形AMOP的面积为12,
∴矩形ABCD的面积为12×4=48,
∵Q、M、P、N分别为矩形四边的中点,
∴四边形PMQN的面积是定值24.
点评 本题考查的是反比例函数综合题,涉及到反比例函数系数k的几何意义及矩形的判定与性质等知识,先根据题意判断出四边形ABCD是矩形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com