Question

如图，A（0，1），M（3，2），N（4，4）.动点P从点A出发，沿轴以每秒1个单位长的速度向上移动，且过点P的直线l：也随之移动，设移动时间为t秒.

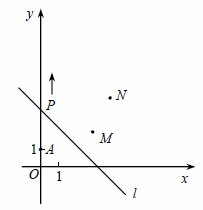
（1）当t＝3时，求l的解析式；

（2）若点M，N位于l的异侧，确定t的取值范围；

（3）直接写出t为何值时，点M关于l的对称点落在坐标轴上.

Answer 1

（1）。

（2）4＜t＜7。

（3）点M关于l的对称点，当t=1时，落在y轴上，当t=2时，落在x轴上

【解析】

分析：（1）利用一次函数图象上点的坐标特征，求出一次函数的解析式。

（2）分别求出直线l经过点M、点N时的t值，即可得到t的取值范围。

（3）找出点M关于直线l在坐标轴上的对称点E、F，如图所示．求出点E、F的坐标，然后分别求出ME、MF中点坐标，最后分别求出时间t的值。

（1）直线交y轴于点P（0，b），

由题意，得b＞0，t≥0，b=1+t，

当t=3时，b=4。

∴当t＝3时， l的解析式为。

（2）当直线过点M（3，2）时，，解得：b=5，

由5=1+t解得t=4。

当直线过点N（4，4）时，，解得：b=8，

由8=1+t解得t=7。

∴若点M，N位于l的异侧，t的取值范围是：4＜t＜7。

（3）如右图，过点M作MF⊥直线l，交y轴于点F，交x轴于点E，则点E、F为点M在坐标轴上的对称点。

过点M作MD⊥x轴于点D，则OD=3，MD=2，

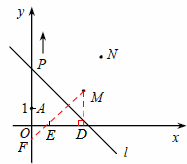
∵∠MED=∠OEF=45°，

∴△MDE与△OEF均为等腰直角三角形。

∴DE=MD=2，OE=OF=1。∴E（1，0），F（0，－1）。

∵M（3，2），F（0，－1），

∴线段MF中点坐标为。

∵直线过点，∴，解得：b=2，

2=1+t，解得t=1。

∵M（3，2），E（1，0），∴线段ME中点坐标为（2，1）。

直线过点（2，1），则，解得：b=3，

3=1+t，解得t=2。

∴点M关于l的对称点，当t=1时，落在y轴上，当t=2时，落在x轴上。