
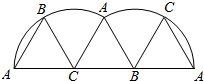
 等边三角形ABC的边长是6厘米,在一条直线上将它翻滚几次,使点A再次落在这条直线上.
等边三角形ABC的边长是6厘米,在一条直线上将它翻滚几次,使点A再次落在这条直线上.分析 (1)点A在翻滚过程中经过的路线总长度就是半径为6厘米、圆心角为120°的弧AA′和弧A′A″的和,也就是求出一段弧的长度,再乘以2,利用弧长公式l=$\frac{nπR}{180}$,代入数据计算即可;
(2)三角形在滚动过程中扫过的面积就是半径为6厘米、圆心角为120°的两个扇形的面积与等边三角形ABC面积的和,利用扇形的面积公式s=$\frac{nπ{R}^{2}}{360}$,代入数据计算即可.
解答 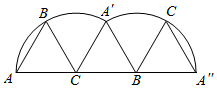 解:(1)$\frac{120×π×6}{180}$×2=8π(厘米);
解:(1)$\frac{120×π×6}{180}$×2=8π(厘米);
答:点A在翻滚的过程中经过的路线总长度是8π厘米.
(2)$\frac{120×π×{6}^{2}}{360}$×2+15=24π+15(平方厘米);
答:三角形在滚动过程中扫过的面积是(24π+15)平方厘米.
点评 本题主要考查了弧长公式和扇形的面积公式的应用.解决的关键是明确点A在翻滚的过程中经过的路线以及三角形在滚动过程中扫过的区域.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
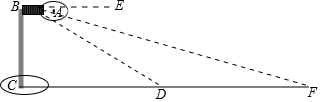
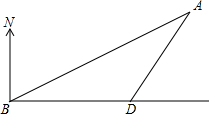 如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?
如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
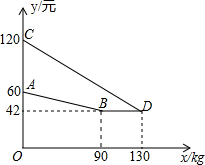 某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABCD、线段CD分别表示该产品每千克生产成本y1(单位:元)销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABCD、线段CD分别表示该产品每千克生产成本y1(单位:元)销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
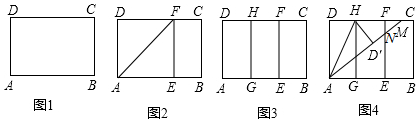
 三国时期吴国赵爽创造了“勾股圆方图”(如图)证明了勾股定理,在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的一个小正方形EFGH组成的,已知小正方形的边长是2,每个直角三角形的短直角边长是6,则大正方形ABCD的面积是100.
三国时期吴国赵爽创造了“勾股圆方图”(如图)证明了勾股定理,在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的一个小正方形EFGH组成的,已知小正方形的边长是2,每个直角三角形的短直角边长是6,则大正方形ABCD的面积是100.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
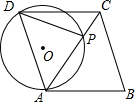 如图,点P在菱形ABCD的对角线AC上,PA=PD,⊙O为△APD的外接圆.
如图,点P在菱形ABCD的对角线AC上,PA=PD,⊙O为△APD的外接圆.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com