
【题目】如图,已知AB为⊙O直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F,cos∠BAC= ![]()

(1)求证:DE是⊙O的切线;
(2)若AF=8,求DF的长.
【答案】
(1)
证明:连接OD,
∵OA=OD,
∴∠ODA=∠OAD,
∵AD平分∠BAC,
∴∠CAD=∠OAD,
∴∠CAD=∠ODA,
∴OD∥AC,
∵AE⊥DE,
∴OD⊥DE,
∵OD为半径,
∴DE是⊙O切线;
(2)
解:过D作DH⊥AB于H,连接BD、OD,
则∠CAB=∠DOH,
∵cos∠DOH=cos∠CAB= ![]() ,
,
设OD=5x,则 AB=10x,OH=3x,DH=4x.
在Rt△ADH中,由勾股定理得:AD2=(4x)2+(5x+3x)2=80x2,
∵DE⊥AC,AB是⊙O直径,
∴∠AED=∠ADB=90°,
∵∠EAD=∠BAD(角平分线定义),
∴△EAD∽△DAB,
∴ ![]() ,
,
∴AD2=AEAB=AE10x,
∴AE=9x,
∵OD∥AE,
∴△ODF∽△EAF,
∴ ![]() ,
,
∵AF=8,
∴DF=5.
【解析】(1)连接OD,推出OD∥AE,推出OD⊥DE,根据切线判定推出即可;(2)连接BD,过D作DH⊥AB于H,根据cos∠DOH=cos∠CAB= ![]() ,设OD=5x,则 AB=10x,OH=3x,DH=4x.由勾股定理得:AD2=80x2 , 证△EAD∽△DAB求出AD2=AEAB=AE10x,得出AE=8x,根据△ODF∽△EAF即可得到结论.
,设OD=5x,则 AB=10x,OH=3x,DH=4x.由勾股定理得:AD2=80x2 , 证△EAD∽△DAB求出AD2=AEAB=AE10x,得出AE=8x,根据△ODF∽△EAF即可得到结论.
【考点精析】关于本题考查的切线的判定定理,需要了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB.
(1)求证:AB是圆的切线;
(2)若点E是BC上一点,已知BE=4,tan∠AEB= ![]() ,AB:BC=2:3,求圆的直径.
,AB:BC=2:3,求圆的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一布袋中有红、黄、白三种颜色的球各一个,它们除颜色外,其它都一样,小亮从布袋摸出一个球后放回去摇匀,再摸出一个球.
(1)请你用列举法(列表法或树形图)分析并求出小亮两次都能摸到白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC.
(1)求证:BE=AF;
(2)若∠ABC=60°,BD=6,求四边形ADEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某过天桥的设计图是梯形ABCD(如图所示),桥面DC与地面AB平行,DC=62米,AB=88米.左斜面AD与地面AB的夹角为23°,右斜面BC与地面AB的夹角为30°,立柱DE⊥AB于E,立柱CF⊥AB于F,求桥面DC与地面AB之间的距离(精确到0.1米)sin23°=0.3907,cos23°=0.9205,tan23°=0.4245![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是将抛物线y=﹣x2平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(﹣1,0),另一个交点为B,与y轴的交点为C.
(1)求抛物线的函数表达式;
(2)若点N为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y= ![]() x+
x+ ![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P,Q的坐标;若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P,Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△DCE是两个全等的等腰三角形,BC,CE为底边.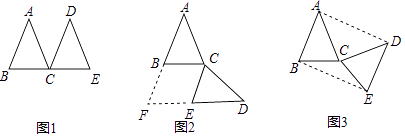

(1)将图1中的△DCE绕C点顺时针方向旋转至∠BCE=∠ACB的位置,分别延长AB,DE交于点F(如图2),此时,四边形BCEF为何种四边形?请证明你的结论;
(2)如果将图1中的△DCE绕C点顺时针旋转至∠BCE=2∠ACB的位置,连接AD,BE(如图3),证明四边形ABED为矩形;
(3)在(2)的条件下,四边形ABED有无可能成为正方形?如果有可能成为正方形,求出∠ABC的度数为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com