
【题目】在平面直角坐标系![]() 中,对于双曲线
中,对于双曲线![]() 和双曲线
和双曲线![]() ,如果
,如果![]() ,则称双曲线
,则称双曲线![]() 和双曲线
和双曲线![]() 为“倍半双曲线”,双曲线
为“倍半双曲线”,双曲线![]() 是双曲线
是双曲线![]() 的“倍双曲线”,双曲线
的“倍双曲线”,双曲线![]() 是双曲线
是双曲线![]() 的“半双曲线”,
的“半双曲线”,

(1)请你写出双曲线![]() 的“倍双曲线”是_____;双曲线
的“倍双曲线”是_____;双曲线![]() 的“半双曲线”是______;
的“半双曲线”是______;
(2)如图1,在平面直角坐标系![]() 中,已知点
中,已知点![]() 是双曲线
是双曲线![]() 在第一象限内任意一点,过点
在第一象限内任意一点,过点![]() 与
与![]() 轴平行的直线交双曲线
轴平行的直线交双曲线![]() 的“半双曲线”于点
的“半双曲线”于点![]() ,求
,求![]() 的面积;
的面积;
(3)如图2,已知点![]() 是双曲线
是双曲线![]() 在第一象限内任意一点,过点
在第一象限内任意一点,过点![]() 与
与![]() 轴平行的直线交双曲线
轴平行的直线交双曲线![]() 的“半双曲线”于点
的“半双曲线”于点![]() ,过点
,过点![]() 与
与![]() 轴平行的直线交双曲线
轴平行的直线交双曲线![]() 的“半双曲线”于点
的“半双曲线”于点![]() ,若
,若![]() 的面积记为
的面积记为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选择:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其他),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):

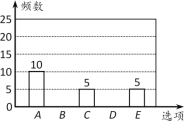
根据以上信息解答下列问题:
⑴ 这次被调查的学生有多少人?
⑵ 表中m的值为 ,并补全条形统计图;
⑶若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂的甲、乙两个车间各生产了400个新款产品,为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围在165≤x<180为合格),分别从甲、乙两个车间生产的产品中随机各抽取了20个样品迸行检测,获得了它们的数据(尺寸),并对数据进行了整理、描述和分析.下面给出了部分信息:
a.甲车间产品尺寸的扇形统计图如下(数据分为6组:165≤x<170,170≤x<175,
175≤x<180,180≤x<185,185≤x<190,190≤x≤195):


b.甲车间生产的产品尺寸在175≤x<180这一组的是:
175 176 176 177 177 178 178 179 179
c.甲、乙两车间生产产品尺寸的平均数、中位数、众数如下:
车间 | 平均数 | 中位数 | 众数 |
甲车间 | 178 | m | 183 |
乙车间 | 177 | 182 | 184 |
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)此次检测中,甲、乙两车间生产的产品合格率更高的是 (填“甲”或“乙”),理由是 ;
(3)如果假设这个工厂生产的所有产品都参加了检测,那么估计甲车间生产该款新产品中合格产品有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张三角形纸片ABC,其中∠C = 90°,AC = 6,BC = 8.如果小明同学将纸片做了两次折叠.第一次使点A落在C处,在纸片上的折痕长记为m;然后将纸片展平做第二次折叠,使点A落在B处,在纸片上的折痕长记为n.那么m,n之间的关系是m_____n.(填“>”,“=”或“<” )
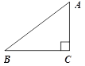
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是![]() 的直径,C点在
的直径,C点在![]() 上,连接AC,
上,连接AC,![]() 的平分线交
的平分线交![]() 于点D,过点D作
于点D,过点D作![]() 交AC的延长线于点E.
交AC的延长线于点E.
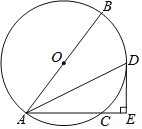
(1)求证:DE是![]() 的切线;
的切线;
(2)若AB=10,![]() ,连接CD,求CD的长.
,连接CD,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
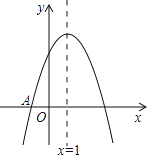
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标
,顶点坐标![]() ,与
,与![]() 轴的交点在点
轴的交点在点![]() 与点
与点![]() 之间(包含端点),则下列结论正确的是( )
之间(包含端点),则下列结论正确的是( )
A.![]()
B.![]()
C.![]() (
(![]() 为任意实数)
为任意实数)
D.方程![]() 有两个不相等的实数根
有两个不相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
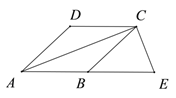
【题目】如图,在菱形ABCD中,CE垂直对角线AC于点C,AB的延长线交CE于点E.
(1)求证:CD=BE;
(2)如果∠E=60°,CE=m,请写出求菱形ABCD面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
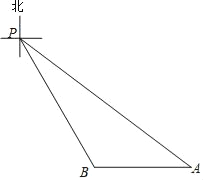
【题目】如图,P点是某海域内的一座灯塔的位置,船A停泊在灯塔P的南偏东53°方向的50海里处,船B位于船A的正西方向且与灯塔P相距20![]() 海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
(1)试问船B在灯塔P的什么方向?
(2)求两船相距多少海里?(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com