Question

6．如图，点E是BC的中点，AB⊥BC，DC⊥BC，AD=AB+CD，AE平分∠BAD，下列结论：①AD=2AE；②∠ADE=∠AEB；③∠AED=90°；④S_△ADE=$\frac{1}{4}$AD•BC中，一定成立的有（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 在AD上截取AF=AB，证明△ABE≌△AFE得BE=FE、∠AFE=∠B=90°、∠AEB=∠AEF=$\frac{1}{2}$∠BEF，再证RT△CDE≌RT△FDE得CE=EF、∠C=∠DFE=90°、∠CED=∠FED=$\frac{1}{2}$∠CEF，根据∠AED=∠AEF+∠DEF可判断③，进而在RT△ADE中可判断①，根据∠DAE=∠EAF、∠AED=∠AFE知∠ADE=∠AEF，可判断②，由EF=BE=CE=$\frac{1}{2}$BC根据三角形面积公式可判断④．

解答 解：如图，在AD上截取AF=AB，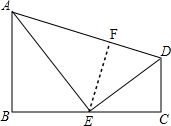

∵AE平分∠BAD，
∴∠BAE=∠FAE，
在△ABE和△AFE中，
∵$\left\{\begin{array}{l}{AB=AE}\\{∠BAE=∠FAE}\\{AE=AE}\end{array}\right.$，
∴△ABE≌△AFE（SAS），
∴AB=AF，BE=FE，∠AFE=∠B=90°，∠AEB=∠AEF=$\frac{1}{2}$∠BEF，
∵AD=AB+CD=AF+DF，
∴CD=DF，
在RT△CDE和RT△FDE中，
∵$\left\{\begin{array}{l}{CD=FD}\\{DE=DE}\end{array}\right.$，
∴RT△CDE≌RT△FDE（HL），
∴CE=EF，∠C=∠DFE=90°，∠CED=∠FED=$\frac{1}{2}$∠CEF，
∴∠AED=∠AEF+∠DEF=$\frac{1}{2}$（∠ABF+∠CEF）=90°，故③正确；
在RT△ADE中，只有当∠ADE=30°时，AD=2AE，故①不一定成立；
在RT△ADE和RT△AEF中，∵∠DAE=∠EAF，∠AED=∠AFE=90°，
∴∠ADE=∠AEF，
∵∠AEF=∠AEB，
∴∠ADE=∠AEB，故②正确；
∵EF=BE=CE=$\frac{1}{2}$BC，
∴S_△ADE=$\frac{1}{2}$AD•EF=$\frac{1}{2}$AD•$\frac{1}{2}$BC=$\frac{1}{4}$AD•BC，故④正确；
则一定成立的有：②③④，
故选：C．

点评 本题主要考查角平分线的性质和判定，证明两对三角形全等是判断结论正确与否的关键．