
| (x1-x2)2+(y1-y2 |
| (2-7)2+(-4-8)2 |
| (x1-x2)2+(y1-y2 |
| (-3-2)2+(-8-4)2 |
| 5 |
| 5 |
| 5 |
| 5 |
| (5-a)2+12 |
| (1-a)2+42 |
| 9 |
| 8 |
| (5-a)2+12 |
| (1-5)2+(4-1)2 |
| 6 |
| 6 |
| (1-a)2+42 |
| (1-5)2+(4-1)2 |
| 9 |
| 8 |
| 6 |
| 6 |


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
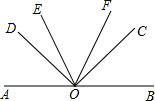 如图,O是直线AB上一点,∠COD=90°,OE平分∠AOC,OF平分∠BOD;
如图,O是直线AB上一点,∠COD=90°,OE平分∠AOC,OF平分∠BOD;查看答案和解析>>
科目:初中数学 来源: 题型:
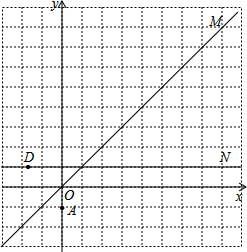 如图,在平面直角坐标系中O为坐标原点,直线OM是一、三象限的角平分线,直线DN是过点(0,1)与x轴平行的直线,一颗棋子从点A(0,-1)处开始依次关于直线OM、直线DN作循环对称变换,即第一次跳到点A关于直线OM的对称点A1处,接着跳到点A1关于直线DN的对称点A2处,第三次再跳到点A2关于直线OM的对称点A3处,….如此下去.
如图,在平面直角坐标系中O为坐标原点,直线OM是一、三象限的角平分线,直线DN是过点(0,1)与x轴平行的直线,一颗棋子从点A(0,-1)处开始依次关于直线OM、直线DN作循环对称变换,即第一次跳到点A关于直线OM的对称点A1处,接着跳到点A1关于直线DN的对称点A2处,第三次再跳到点A2关于直线OM的对称点A3处,….如此下去.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
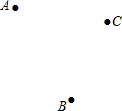 如图,点 A、B、C表示三个自然村庄,自来水公司准备在其间建一水厂P,要求水厂P到三个村的距离相等.请你用“尺规作图”帮自来水公司找到P的位置(不要求写出作法但要保留作图痕迹).
如图,点 A、B、C表示三个自然村庄,自来水公司准备在其间建一水厂P,要求水厂P到三个村的距离相等.请你用“尺规作图”帮自来水公司找到P的位置(不要求写出作法但要保留作图痕迹).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com