Question

13．在△ABC中，BD平分∠ABC（∠ABC＜60°）
（1）如图1，当点D在AC边上时，若∠ABC=42°，∠ACB=32°，请直接写出AB，DC和BC之间的数量关系．
（2）如图2，当点D在△ABC内部，且∠ACD=30°时，
①若∠BDC=150°，直接写出AB，AD和BC之间的数量关系，并写出结论成立的思路．
②若∠ABC=2α，∠ACB=60°-α，请直接写出∠ADB的度数（用含α的式子表示）．

Answer 1

分析 （1）在BC上截取BE=BA，连接DE，由三角形内角和定理求出∠A=180°-∠ABC-∠ACB=106°，由角平分线得出∠1=∠2=$\frac{1}{2}$∠ABC=21°，由SAS证明△BDE≌△BDA，得出∠BED=∠A=106°，∠CED=74°，再由三角形的外角性质得出∠CDE=∠CED，证出CE=CD，即可得出结论；
（2）①延长BA到点E，使BE=BC，连接ED，EC，由SAS证明△BED≌△BCD，得出DE=DC，∠BDE=∠BDC=150°，证出△CDE为等边三角形，得出∠ACE=∠ACD=30°，AC垂直平分DE．由线段垂直平分线的性质得出AD=AE，即可得出结论；
②同①，延长BA到点E，使BE=BC，连接ED，EC，由三角形内角和定理求出∠BDC=150°，由SAS证明△BED≌△BCD，得出DE=DC，∠BDE=∠BDC=150°，∠BED=∠BCD=30°-α，证出△CDE为等边三角形，得出∠ACE=∠ACD=30°，AC垂直平分DE．证出AD=AE，得出∠ADE=∠BED=30°-α，即可求出∠ADB=120°+α．

解答 解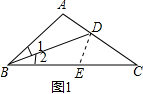：（1）BC=AB+DC，理由如下：
在BC上截取BE=BA，连接DE，如图1所示：
∵∠ABC=42°，∠ACB=32°，
∴∠A=180°-∠ABC-∠ACB=106°，
∵BD平分∠ABC，
∴∠1=∠2=$\frac{1}{2}$∠ABC=21°，
在△BDE和△BDA中，$\left\{\begin{array}{l}{BE=BA}&{\;}\\{∠2=∠1}&{\;}\\{BD=BD}&{\;}\end{array}\right.$，
∴△BDE≌△BDA（SAS），
∴∠BED=∠A=106°，
∴∠CED=180°-106°=74°，
∵∠BED=∠C+∠CDE，
∴∠CDE=∠BED-∠C=74°=∠CED，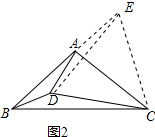
∴CE=CD，
∴BC=BE+CE=AB+CD；
（2）①BC=AB+AD，思路如下：
延长BA到点E，使BE=BC，连接ED，EC，如图2所示：
∵BD平分∠ABC，
∴∠ABD=∠CBD，
∵BD=BD，
∴△BED≌△BCD（SAS），
∴DE=DC，∠BDE=∠BDC=150°
∴∠EDC=360°-150°-150°=60°，
∴△CDE为等边三角形，
∵∠ACD=30°，
∴∠ACE=∠ACD=30°
∴AC垂直平分DE．
∴AD=AE，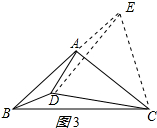
∴BC=BE=AB+AE=AB+AD；
②∠ADB=120°+α．理由如下：
同①，延长BA到点E，使BE=BC，连接ED，EC，如图3所示：
∵∠ACD=30°，∠ACB=60°-α，
∴∠BCD=30°-α，
∵BD平分∠ABC，
∴∠ABD=∠CBD=α，
∴∠BDC=180°-∠CBD-∠BCD=180°-α-（30°-α）=150°，
∵BD=BD，
∴△BED≌△BCD（SAS），
∴DE=DC，∠BDE=∠BDC=150°，∠BED=∠BCD=30°-α，
∴∠EDC=360°-150°-150°=60°，
∴△CDE为等边三角形，
∵∠ACD=30°，
∴∠ACE=∠ACD=30°，
∴AC垂直平分DE．
∴AD=AE，
∴∠ADE=∠BED=30°-α，
∴∠ADB=150°-（30°-α）=120°+α．

点评 本题是三角形综合题目，考查了全等三角形的判定与性质、等边三角形的判定与性质、线段垂直平分线的性质、三角形的外角性质、三角形内角和定理、等腰三角形的性质等知识；本题综合性强，有一定难度，证明三角形全等和等边三角形是解决问题的关键．