
如图1,抛物线![]() :
:![]() 与直线AB:
与直线AB:![]() 交于x轴上的一点A,和另一点B(3,n).
交于x轴上的一点A,和另一点B(3,n).
(1)求抛物线![]() 的解析式;
的解析式;
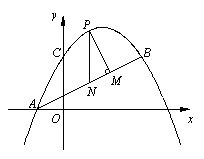
(2)点P是抛物线![]() 上的一个动点(点P在A,B两点之间,但不包括A,B两点),PM⊥AB于点M,PN∥y轴交AB于点N,在点P的运动过程中,存在某一位置,使得△PMN的周长最大,求此时P点的坐标,并求△PMN周长的最大值;
上的一个动点(点P在A,B两点之间,但不包括A,B两点),PM⊥AB于点M,PN∥y轴交AB于点N,在点P的运动过程中,存在某一位置,使得△PMN的周长最大,求此时P点的坐标,并求△PMN周长的最大值;
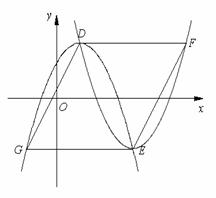
(3)如图2,将抛物线![]() 绕顶点旋转180°后,再作适当平移得到抛物线
绕顶点旋转180°后,再作适当平移得到抛物线![]() ,已知抛物线
,已知抛物线![]() 的顶点E在第四象限的抛物线
的顶点E在第四象限的抛物线![]() 上,且抛物线
上,且抛物线![]() 与抛物线
与抛物线![]() 交于点D,过D点作
交于点D,过D点作![]() 轴的平行线交抛物线
轴的平行线交抛物线![]() 于点F,过E点作
于点F,过E点作![]() 轴的平行线交抛物线
轴的平行线交抛物线![]() 于点G,是否存在这样的抛物线
于点G,是否存在这样的抛物线![]() ,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在请说明理由.
,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在请说明理由.
、
解:⑴由题意得:A(-1,0)、B(3,2)
∴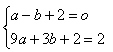 解得:
解得: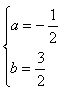 ∴抛物线的解析式为y=-
∴抛物线的解析式为y=-![]() x+
x+![]() x+2
x+2
⑵设AB交y轴于D,则D(0,![]() ),∴OA=1,OD=
),∴OA=1,OD=![]() ,AD=
,AD=![]() ,∴
,∴![]() =
=![]() ,
,
∵PN∥y轴, ∴∠PNM=∠CDN=∠ADO, ∴Rt△ADO∽Rt△PNM.
∴![]() .∴
.∴![]() =
=![]() ×
×![]() PN=
PN=![]() PN.
PN.
∴当PN取最大值时, ![]() 取最大值.
取最大值.
设P(m, -![]() m+
m+![]() m+2) N(m,
m+2) N(m, ![]() m+
m+![]() ).则PN=-
).则PN=-![]() m+
m+![]() m+2-(
m+2-(![]() m+
m+![]() )=-
)=-![]() m+m+
m+m+![]() .
.
∵-1﹤m﹤3. ∴当m=1时,PN取最大值.
∴△PNM周长的最大值为![]() ×2=
×2=![]() .此时P(1,3).
.此时P(1,3).
⑶设E(n,t),由题意得:抛物线![]() 为:y=-
为:y=-![]() (x-
(x-![]() )+
)+![]() ,
,![]() 为:y=
为:y=![]() (x-n) +t.
(x-n) +t.
∵E在抛物线![]() 上,∴t=-
上,∴t=-![]() (n-
(n-![]() )
)![]() +
+![]() .∵四边形DFEG为菱形. ∴DF=FE=EG=DG
.∵四边形DFEG为菱形. ∴DF=FE=EG=DG
连ED,由抛物线的对称性可知,ED=EF.∴△DEG与△DEF均为正三角形.∴D为抛物线![]() 的顶点.∴D(
的顶点.∴D(![]() ,
,![]() ).∵DF∥x轴,且D、F关于直线x=n对称.∴DF=2(n-
).∵DF∥x轴,且D、F关于直线x=n对称.∴DF=2(n-![]() ).
).
∵DEF为正三角形.∴![]() -
-![]() =
=![]() ×2(n-
×2(n-![]() ).解得:n=
).解得:n=![]() .
.
∴t=-![]() .∴存在点E,坐标为E(
.∴存在点E,坐标为E(![]() ,-
,-![]() ).
).


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:湖南省中考真题 题型:解答题


查看答案和解析>>
科目:初中数学 来源:2012年河北省承德三中中考数学模拟试卷(二)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2012年浙江省杭州市中考数学模拟试卷(五)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com