
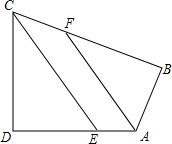
 如图,四边形ABCD中CD⊥DA,CE平分∠DCB交AD于E,AF平分∠DAB交BC于F,CE∥FA,求∠B.
如图,四边形ABCD中CD⊥DA,CE平分∠DCB交AD于E,AF平分∠DAB交BC于F,CE∥FA,求∠B. 分析 根据角平分线的性质得到∠BCD=2∠ECD,∠BAD=2∠FAD,根据AF∥CE,得到∠FAD=∠CED,由∠D=90°,从而得到∠ECD+∠EDC=90°,可得∠BAC+∠BCD=2(∠FAD+∠ECD)=180°,再根据四边形内角和为360°,即可解答.
解答 解:∵CE、AF分别平分∠BCD、∠BAD,
∴∠BCD=2∠ECD,∠BAD=2∠FAD,
∵AF∥CE,
∴∠FAD=∠CED,
∵CD⊥DA,
∴∠D=90°,
∴∠ECD+∠EDC=90°,
∴∠BAC+∠BCD=2(∠FAD+∠ECD)
=2(∠CED+∠ECD)
=2×90°
=180°,
根据四边形内角和为360°得:
∠B=360°-(∠BAD+∠BCD)-∠D=360°-180°-90°=90°.
点评 本题考查了平行线的性质、角平分线的性质、多性质边形的内角和,解决本题的关键是熟记平行线的性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
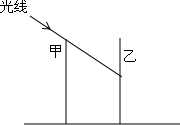 如图,甲、乙两楼的高都为30m,两楼相距24m,在某一时刻太阳光线与水平线的夹角为30°,则甲楼的影子落在乙楼上的高度为(30-8$\sqrt{3}$)m.
如图,甲、乙两楼的高都为30m,两楼相距24m,在某一时刻太阳光线与水平线的夹角为30°,则甲楼的影子落在乙楼上的高度为(30-8$\sqrt{3}$)m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
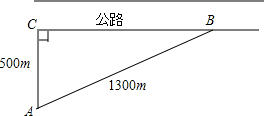 我方侦查员小王在距离东西向500米处公路侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距500米,30秒后,汽车与他相距1300米,请你帮小王计算敌方汽车的速度吗?
我方侦查员小王在距离东西向500米处公路侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距500米,30秒后,汽车与他相距1300米,请你帮小王计算敌方汽车的速度吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com