
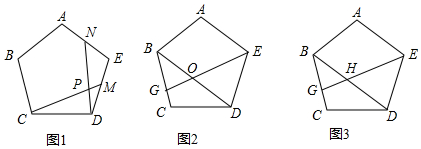
分析 (1)首先证明△CDM≌△DEN,可得∠DCM=∠NDE,∠CMD=∠DNE,CM=DN,由△MPD∽△MDC,可得DM2=MP•MC,由△DPM∽△DEN,可得$\frac{DP}{PM}$=$\frac{DE}{EN}$=2,推出PM=$\frac{1}{2}$PD,由此即可解决问题;
(2)如图2中,连接BE,延长EG交DC的延长线于H,在EB上取一点M,使得EM=AE,连接AM,设AB=AE=CD=EM=a,BM=x.由△ABM∽△EBA,可得AB2=BM•BE,即a2=x(x+a),解得$\frac{x}{a}$=$\frac{\sqrt{5}-1}{2}$或$\frac{-\sqrt{5}-1}{2}$(舍弃),推出$\frac{BE}{BM}$=$\frac{3+\sqrt{5}}{2}$易知BE∥DH,可得$\frac{OB}{OD}$=$\frac{BE}{DH}$=1,推出BE=DH,由CD=EM,推出CH=BM,可得$\frac{BG}{GC}$=$\frac{BE}{CH}$=$\frac{BE}{BM}$,由此即可解决问题;
(3)如图3中,连接BE,延长EG交DC的延长线于M.由AB=$\sqrt{5}$+1,由(2)可知,BE=BD=$\sqrt{5}$+3,由BE∥DM,可得$\frac{BG}{GC}$=$\frac{BE}{CM}$=1,推出BE=CM=$\sqrt{5}$+3,推出DM=$\sqrt{5}$+3+$\sqrt{5}$+1=2$\sqrt{5}$+4,由$\frac{BH}{HD}$=$\frac{BE}{DM}$=$\frac{\sqrt{5}+3}{2\sqrt{5}+4}$,推出$\frac{BH}{BD}$=$\frac{\sqrt{5}+3}{3\sqrt{5}+7}$,由此即可求出BH;
解答 (1)证明:如图1中,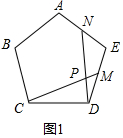
∵ABCDE是正五边形,
∴CD=DE=AE,∠CDM=∠DEN,
∵AN=NE,DM=EM.
∴DM=EN,
∴△CDM≌△DEN,
∴∠DCM=∠NDE,∠CMD=∠DNE,CM=DN,
∵∠PMD=∠DMC,
∴△MPD∽△MDC,
∴$\frac{MP}{DM}$=$\frac{DM}{MC}$,
∴DM2=MP•MC,
∵∠DMP=∠DNE,∠PDM=∠NDE,
∴△DPM∽△DEN,
∴$\frac{DP}{DE}$=$\frac{PM}{EN}$,
∴$\frac{DP}{PM}$=$\frac{DE}{EN}$=2,
∴PM=$\frac{1}{2}$PD,
∵DM2=$\frac{1}{4}$DE2,
∴$\frac{1}{4}$DE2=$\frac{1}{2}$DP•CM,
∵CM=DN,
∴$\frac{1}{2}$DE2=DP•DN.
(2)解:如图2中,连接BE,延长EG交DC的延长线于H,在EB上取一点M,使得EM=AE,连接AM,设AB=AE=CD=EM=a,BM=x.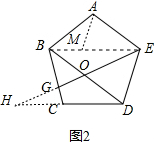
∵∠BAE=108°,∠AEB=36°,EA=EM,
∴∠EAM=∠EMA=72°,∠BAM=36°,
∴∠BAM=∠BEA,∵∠ABM=∠ABE,
∴△ABM∽△EBA,
∴AB2=BM•BE,
∴a2=x(x+a),
可得:($\frac{x}{a}$)2+$\frac{x}{a}$-1=0,
解得$\frac{x}{a}$=$\frac{\sqrt{5}-1}{2}$或$\frac{-\sqrt{5}-1}{2}$(舍弃),
∴$\frac{BM}{ME}$=$\frac{\sqrt{5}-1}{2}$,
∴$\frac{BE}{BM}$=$\frac{3+\sqrt{5}}{2}$
易知BE∥DH,
∴$\frac{OB}{OD}$=$\frac{BE}{DH}$=1,
∴BE=DH,
∵CD=EM,
∴CH=BM,
∴$\frac{BG}{GC}$=$\frac{BE}{CH}$=$\frac{BE}{BM}$=$\frac{3+\sqrt{5}}{2}$.
(3)解:如图3中,连接BE,延长EG交DC的延长线于M.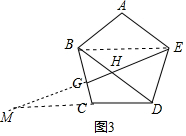
∵AB=$\sqrt{5}$+1,由(2)可知,BE=BD=$\sqrt{5}$+3,
∵BE∥DM,
∴$\frac{BG}{GC}$=$\frac{BE}{CM}$=1,
∴BE=CM=$\sqrt{5}$+3,
∴DM=$\sqrt{5}$+3+$\sqrt{5}$+1=2$\sqrt{5}$+4,
∵$\frac{BH}{HD}$=$\frac{BE}{DM}$=$\frac{\sqrt{5}+3}{2\sqrt{5}+4}$,
∴$\frac{BH}{BD}$=$\frac{\sqrt{5}+3}{3\sqrt{5}+7}$,
∴BH=2.
点评 本题考查四边形综合题、相似三角形的判定和性质、平行线分线段成比例定理、一元二次方程等知识,解题的关键是学会添加常用辅助线,学会利用参数解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
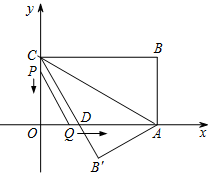 如图,在平面直角坐标系中,矩形OABC的顶点A的坐标为(6,0),将△ABC沿AC翻折,使点B落到点B′处,B′C交x轴于点D,且CD=2DB′.动点P从点C出发,沿CO以每秒1个单位的速度向点O运动;动点Q从点O出发,沿OA、AB以每秒3个单位的速度向点B运动,连接PQ.若P、Q两点同时出发,当其中一点到达终时整个运动随之结束,设运动时间为t秒.
如图,在平面直角坐标系中,矩形OABC的顶点A的坐标为(6,0),将△ABC沿AC翻折,使点B落到点B′处,B′C交x轴于点D,且CD=2DB′.动点P从点C出发,沿CO以每秒1个单位的速度向点O运动;动点Q从点O出发,沿OA、AB以每秒3个单位的速度向点B运动,连接PQ.若P、Q两点同时出发,当其中一点到达终时整个运动随之结束,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
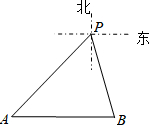 如图,某天上午,一渔船在我海上指挥中心P的南偏东15°方向的B处遇险,在海上指挥中心P的南偏西45°方向A处的海口舰接到求救信号后立刻前往救援,此时,海口舰与指挥中心P相距10($\sqrt{3}$+1)海里,渔船B在海口舰A的正东方向.求此时渔船B与海口舰A的距离(结果保留根号).
如图,某天上午,一渔船在我海上指挥中心P的南偏东15°方向的B处遇险,在海上指挥中心P的南偏西45°方向A处的海口舰接到求救信号后立刻前往救援,此时,海口舰与指挥中心P相距10($\sqrt{3}$+1)海里,渔船B在海口舰A的正东方向.求此时渔船B与海口舰A的距离(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
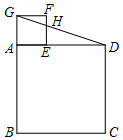 如图,在正方形ABCD和正方形AEFG中,顶点E在边AD上,连接DG交EF于点H,若FH=1,EH=2,则DG的长为$3\sqrt{10}$.
如图,在正方形ABCD和正方形AEFG中,顶点E在边AD上,连接DG交EF于点H,若FH=1,EH=2,则DG的长为$3\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
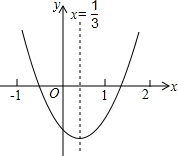 从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0; ②abc>0 ③a-b+c>0 ④2a+b>0 ⑤4a+2b+c<0.你认为其中正确的信息个数有( )
从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0; ②abc>0 ③a-b+c>0 ④2a+b>0 ⑤4a+2b+c<0.你认为其中正确的信息个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com