
【题目】在![]() 中,以
中,以![]() 为斜边,作直角
为斜边,作直角![]() ,使点
,使点![]() 落在
落在![]() 内,
内, ![]() .
.
(1)如图1,若![]() ,
, ![]() ,
, ![]() ,点
,点![]() 分别为
分别为![]() 、
、![]() 边的中点,连接
边的中点,连接![]() ,求线段
,求线段![]() 的长;
的长;
(2)如图2,若![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转一定角度,得到
逆时针旋转一定角度,得到![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证: ![]() ;
;
(3)如图3,若![]() ,过点
,过点![]() 的直线交
的直线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
, ![]() ,且
,且![]() ,请直接写出线段
,请直接写出线段![]() 之间的关系(不需要证明).
之间的关系(不需要证明).

【答案】(1)PM=7;(2)证明见解析;(3)BP=CP
【解析】试题分析:(1)根据直角三角形30度角性质求出AB,再根据三角形中位线定理即可求出PM.
(2)如图2中,在ED上截取EQ=DP,连接CQ.首先证明△EQC≌△DPB,推出QC=PB,再证明QC=PC即可解决问题.
(3)结论:2AD2=FB2+CF2.如图3中,连接AF交BD于N.由△AND∽△BNF,推出![]() ,推出
,推出![]() ,又∠ANB=∠DNF,推出△ANB∽△DNF,从∠DFN=∠ABD=45°,在RtABF中利用勾股定理即可证明.
,又∠ANB=∠DNF,推出△ANB∽△DNF,从∠DFN=∠ABD=45°,在RtABF中利用勾股定理即可证明.
试题解析:(1)如图1中,
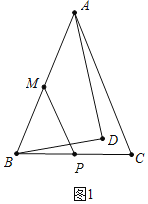
∵∠ADB=90°,∠DBA=60°,AD=![]() ,
,
∴∠BAD=30°,
∴AB=2BD,设BD=a,则AB=2a,
∵AB2=BD2+AD2,
∴(2a)2=a2+(![]() )2,
)2,
∴a=7,
∴AB=AC=14,
∵AM=MB,PB=PC,
∴PM=![]() AC=7.
AC=7.
(2)证明:如图2中,在ED上截取EQ=DP,连接CQ.
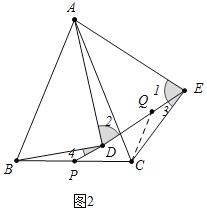
∵AD=AE,
∴∠1=∠2,
∵∠ADB=∠AEC=90°,
∴∠1+∠3=90°,∠2+∠4=90°,
∴∠3=∠4,
∵BD=EC,
∴△EQC≌△DPB,
∴CQ=BP,∠QCE=∠DBP,
∵∠CQP=∠3+∠QCE,∠CPQ=∠4+∠DBP,
∴∠CQP=∠CPQ,
∴CQ=PC,
∴PB=PC.
(3)结论:2AD2=FB2+CF2.
理由:如图3中,连接AF交BD于N.
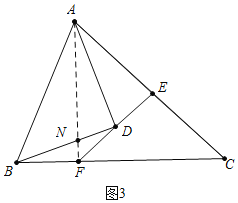
∵∠ADB=90°,DA=DB,
∴∠DBA=∠DAB=45°,AB=![]() AD,
AD,
∵∠AND=∠BNF,∠ADN=∠BFN=90°,
∴△AND∽△BNF,
∴![]() ,
,
∴![]() ,
,
∵∠ANB=∠DNF,
∴△ANB∽△DNF,
∴∠DFN=∠ABD=45°,
∵FE⊥AC,AE=EC,
∴FA=FC,∠AFE=∠CFE=45°,
∴∠AFC=∠AFB=90°,
∴AB2=BF2+AF2,
∴2AD2=BF2+CF2.


科目:初中数学 来源: 题型:
【题目】清明节是祭祖和扫墓的日子,据宁波市民政局社会事务处的数据显示,今年清明期间全市祭扫人数超300万人次,其中的300万用科学记数法表示为( )
A.3×105
B.3×106
C.30×105
D.0.3×106
查看答案和解析>>
科目:初中数学 来源: 题型:
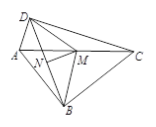
【题目】如图,四边形ABCD中,∠ABC=90°,BD的垂直平分线交AC、BD分别于点M、N,点M为AC中点.
(1) 求证:AM=DM;
(2) 求∠ADC的度数;
(3) 当∠BCD为_______°时,∠BMD为120°.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A. 线段是轴对称图形
B. 等边三角形有3条对称轴
C. 角只有一条对称轴,是这个角的角平分线
D. 底与腰不相等的等腰三角形只有一条对称轴
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交BC、AC于点D、E.
(1)若AC=12,BC=15,求△ABD的周长;
(2)若∠B=20°,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号__________.
①∠ODE=∠ODF;②∠OED=∠OFD;③ED=FD;④EF⊥OC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界最大的500米口径球面射电望远镜(FAST)于2016年9月25日在贵州省平塘县落成启用,被誉为“中国天眼”,能够接收到137亿光年以外的电磁信号137亿用科学记数法表示为( )
A.137×108
B.1.37×109
C.1.37×1010
D.1.37×1011
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com