
【题目】若一条直线把一个平面图形分成面积相等的两部分,那么这条直线叫做该平面图形的“和谐线”,其“和谐线”被该平面图形截得的线段叫做该平面图形的“和谐线段”(例如圆的直径就是圆的“和谐线段”)
问题探究:
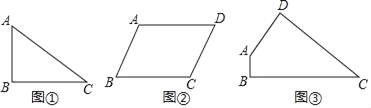
(1)如图①,已知△ABC中,AB=6,BC=8,∠B=90°,请写出△ABC的两条“和谐线段”的长.
(2)如图②,平行四边形ABCD中,AB=6,BC=8,∠B=60°,请直接写出该平行四边形ABCD的“和谐线段”长的最大值和最小值;
问题解决
(3)如图③,四边形ABCD是某市规划中的商业区示意图,其中AB=2,CD=10,∠A=135°,∠B=90°,tanC=![]() ,现计划在商业区内修一条笔直的单行道MN(小道的宽度不计),入口M在BC上,出口N在CD上,使得MN为四边形ABCD“和谐线段”,在道路一侧△MNC区域规划为公园,为了美观要求△MNC是以CM为腰的等腰三角形,请通过计算说明设计师的想法能否实现?若可以,请确定点M的位置(即求CM的长).
,现计划在商业区内修一条笔直的单行道MN(小道的宽度不计),入口M在BC上,出口N在CD上,使得MN为四边形ABCD“和谐线段”,在道路一侧△MNC区域规划为公园,为了美观要求△MNC是以CM为腰的等腰三角形,请通过计算说明设计师的想法能否实现?若可以,请确定点M的位置(即求CM的长).
【答案】(1)BD=5,AE=2![]() ,CF=
,CF=![]() ;(2)最小值为3
;(2)最小值为3![]() ,最大值为2
,最大值为2![]() ;(3)可以,CM的值为
;(3)可以,CM的值为![]()
【解析】
(1)作△ABC的中线AE,BD,CF.线段AE,BD,CF都是△ABC的和谐线段.
(2)作AE⊥BC于E,CF⊥AB于F,连接AC,BD交于点O.经过点O的直线都是平行四边形ABCD的“和谐线”.求出平行四边形对边之间的距离,对角线的从即可判断.
(3)构造直角三角形,求出四边形ABCD的面积,分两种情形分别求解即可.
(1)作△ABC的中线AE,BD,CF.线段AE,BD,CF都是△ABC的和谐线段.

在Rt△ABC中,∵∠ABC=90°,AB=6,BC=8,
∴AC=![]() =10,
=10,
∴BD=![]() AC=5,AE=
AC=5,AE=![]() =2
=2![]() ,CF=
,CF=![]() =
=![]() .
.
(2)作AE⊥BC于E,CF⊥AB于F,连接AC,BD交于点O.经过点O的中线都是平行四边形ABCD的“和谐线”.
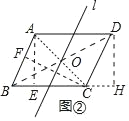
在Rt△ABE中,∵∠AEB=90°,AB=6,∠ABE=60°,
∴AE=ABsin60°=3![]() ,
,
同法可求:CF=4![]() ,
,
∴平行四边形ABCD的“和谐线段”长的最小值为3![]() ,
,
作DH⊥BC交BC的延长线于H.易知CH=BE=3,
在Rt△BDH中,BD=![]() =
=![]() =2
=2![]() ,
,
在Rt△ACE中,AC=![]() =
=![]() =2
=2![]() ,
,
∴平行四边形ABCD的“和谐线段”长的最大值为2![]() .
.
(3)如图③﹣1中,作DE⊥BC于E,AF⊥DE于F.
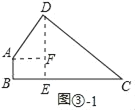
在Rt△CDE中,∵CD=10,tanC=![]() ,
,
∴DE=6,EC=8,
∵四边形ABEF是矩形,
∴AB=EF=2,
∴DF=4,
∵∠DAB=135°,∠BAF=90°,
∴∠DAF=45°,
∴AF=BE=DF=4,
∴BC=4+8=12,
∴S四边形ABCD=![]() (2+6)×4+
(2+6)×4+![]() ×6×8=40,
×6×8=40,
如图③﹣2中,当CM=CN时,设CM=CN=x.
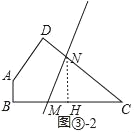
∵tanC=![]() =
=![]() ,
,
∴NH=![]() x,
x,
∵S△MNC=20,
∴![]()
![]() xx=20,
xx=20,
∴x=![]() 或﹣
或﹣![]() (舍弃).
(舍弃).
如图③﹣3中,当CM=MN时,设CM=MN=x.作MH⊥CN于H.

∵MC=MN,MH⊥CN,
∴CH=HN,
∵tanC=![]() =
=![]() ,
,
∴MH=![]() x,CH=
x,CH=![]() x,
x,
∴CN=![]() x,
x,
∴![]()
![]() x
x![]() x=20,
x=20,
∴x=![]() 或(﹣
或(﹣![]() )
)
此时CN>10,不符合题意舍弃,
综上所述,满足条件的CM的值为![]() .
.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
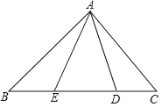
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=_____(用含a、b的式子表示AB).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图l、图2均为8×6的方格纸(每个小正方形的边长均为1),在方格纸中各有一条线段AB,其中点A、B均在小正方形的顶点上,请按要求画图:

(1)在图l中画一直角△ABC,使得tan∠BAC=![]() ,点C在小正方形的顶点上;
,点C在小正方形的顶点上;
(2)在图2中画一个□ABEF,使得□ABEF的面积为图1中△ABC面积的4倍,点E、F在小正方形的顶点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为90元的新商品,在商场试销时发现:销售单价![]() 元
元![]() 件
件![]() 与每天销售量
与每天销售量![]() 件
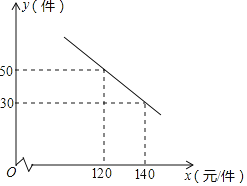
件![]() 之间满足如图所示的关系.
之间满足如图所示的关系.
![]() 求出y与x之间的函数关系式;
求出y与x之间的函数关系式;
![]() 写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
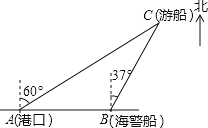
【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知某小区的两幢10层住宅楼间的距离为AC="30" m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3 m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α .
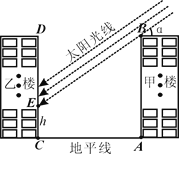
(1) 用含α的式子表示h(不必指出α的取值范围);
(2) 当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光 ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市2016年中考,综合素质测试满分为100分.某校为了调查学生对于综合素质的掌握程度,在九年级学生中随机抽取了部分学生进行模拟测试,并将测试成绩绘制成下面两幅统计图.
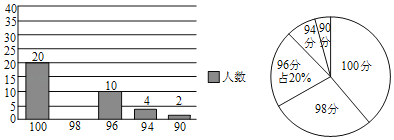
试根据统计图中提供的数据,回答下面问题:
(1)计算样本中,成绩为98分的学生有 ,并补全条形统计图.
(2)样本中,测试成绩的中位数是 分,众数是 分.
(3)若该校九年级共有2000名学生,根据此次模拟成绩估计该校九年级中考综合素质测试将有多少名学生可以获得满分.
查看答案和解析>>
科目:初中数学 来源: 题型:
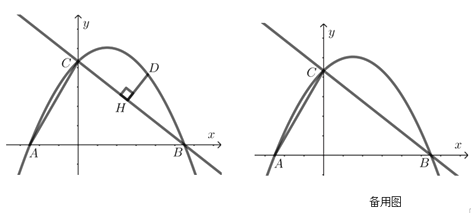
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点B,与y轴交于点C,抛物线
与x轴交于点B,与y轴交于点C,抛物线![]() 经过点B和点C,且与x轴交于另一点A,连接AC,点D在BC上方的抛物线上,设点D的横坐标为m,过点D作DH⊥BC于点H.
经过点B和点C,且与x轴交于另一点A,连接AC,点D在BC上方的抛物线上,设点D的横坐标为m,过点D作DH⊥BC于点H.
(1)求抛物线的函数表达式;
(2)线段DH的长为 (用含m的代数式表示);
(3)点M为线段AC上一点,连接OM绕点O顺时针旋转60°得线段ON,连接CN,当CN=![]() ,m=6时,请直接写出此时线段DM的长.
,m=6时,请直接写出此时线段DM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
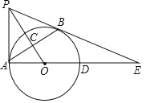
【题目】如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求PB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com