
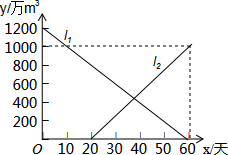
 今年夏天,重庆各区持续高温日数达到历史之最,受持续高温和连日无雨的影响,重庆某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其他因素).若总蓄水量不多于900万m3为严重干旱,则该水库发生严重干旱时的天数为15≤x≤40天.
今年夏天,重庆各区持续高温日数达到历史之最,受持续高温和连日无雨的影响,重庆某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其他因素).若总蓄水量不多于900万m3为严重干旱,则该水库发生严重干旱时的天数为15≤x≤40天. 分析 分两种情况:①当0≤x≤20时,y=y1,②当20<x≤60时,y=y1+y2;并计算分段函数中y≤900时对应的x的取值.
解答 解:设y2=kx+b,
把(20,0)和(60,1000)代入到y2=kx+b中得:
$\left\{\begin{array}{l}{20k+b=0}\\{60k+b=1000}\end{array}\right.$ 解得$\left\{\begin{array}{l}{k=25}\\{b=-500}\end{array}\right.$,
∴y2=25x-500,
当0≤x≤20时,y=-20x+1200,
当20<x≤60时,y=y1+y2=-20x+1200+25x-500=5x+700,
y≤900,则5x+700≤900,
x≤40,
当y1=900时,900=-20x+1200,
x=15,
∴发生严重干旱时x的范围为:15≤x≤40.
故答案为:15≤x≤40
点评 本题考查了一次函数的应用,熟练掌握利用待定系数法求一次函数的解析式:设直线解析式为y=kx+b,将直线上两点的坐标代入列二元一次方程组,求解;注意分段函数的实际意义,会观察图象.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | 合计 |
| -25.6 | -72.7 | 200 | -4 | 128.3 | 168 | 494 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com