
(本题6分) 我们已经知道,利用面积的不同表示方法可以写出一个代数恒等式,例如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图1的图形面积的不同表示方法来表示。
(1)请写出图2所解释的代数恒等式:________________________;
(2)利用上述方法画出一个几何图形说明代数恒等式:(a+3b)(a+b)=a2+4ab+3b2的正确性。
|
a2 |
a2 |
ab |
|
ab |
ab |
b2 |
|
ab |
ab |
b2 |

|
a2 |
a2 |
ab |
|
ab |
ab |
b2 |
解:
科目:初中数学 来源: 题型:
、(本题10分)我们知道,对于二次函数y=a(x+m)2+k的图像,可由函数y=ax2的图像 进行向左或向右平移一次、再向上或向下移一次平移得到,我们称函数y=ax2为“基本函数”,而称由它平移得到的二次函数y=a(x+m)2+k为“基本函数”y=ax2的“朋友函数”。左右、上下平移的路径称为朋友路径,对应点之间的线段距离![]() 称为朋友距离。
称为朋友距离。
由此,我们所学的函数:二次函数y=ax2,函数y=kx和反比例函数![]() 都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”。
都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”。
如一次函数y=2x-5是基本函数y=2x的朋友函数,由y=2x-5=2(x-1)-3朋友路径可以是向右平移1个单位,再向下平移3个单位,朋友距离=![]() .
.
1.(1)探究一:小明同学经过思考后,为函数y=2x-5又找到了一条朋友路径为由基本函数y=2x先向 ,再向下平移7单位,相应的朋友距离为 。
2.(2)探究二:已知函数y=x2-6x+5,求它的基本函数,朋友路径,和相应的朋友距离。
3.(3)探究三:为函数![]() 和它的基本函数
和它的基本函数![]() ,找到朋友路径,
,找到朋友路径,
并求相应的朋友距离。
查看答案和解析>>
科目:初中数学 来源: 题型:
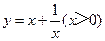
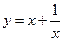
| x | …… | 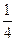 | 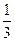 | 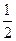 | 1 | 2 | 3 | 4 | …… |
| y | …… | | | | | | | | …… |
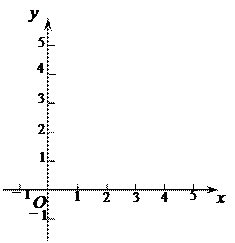
|
查看答案和解析>>
科目:初中数学 来源:2014届浙江省建德市八年级3月月考数学试卷(解析版) 题型:解答题
(本题8分)
阅读材料:如果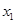 、
、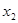 是一元二次方程
是一元二次方程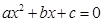 (
( ≠0)的两根,那么,
≠0)的两根,那么,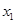 +
+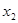 =
=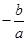 ,
,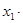
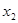 =
=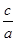 .这就是著名的韦达定理.
.这就是著名的韦达定理.
现在我们利用韦达定理解决问题:
已知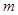 与
与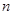 是方程
是方程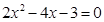 的两根,
的两根,
(1)填空: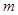 +
+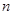 =________;
=________;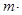
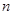 =________;
=________;
(2)计算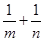 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年上海市闸北区中考一模数学试卷(解析版) 题型:解答题
(本题满分10分 第(1)小题4分,第(2)小题6分)
已知:二次函数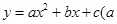 ≠0的图像经过点(3,5)、(2,8)、(0,8).
≠0的图像经过点(3,5)、(2,8)、(0,8).
(1)求这个二次函数的解析式;
(2)已知抛物线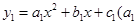 ≠0,
≠0,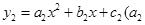 ≠0,且满足
≠0,且满足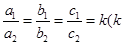 ≠0,1,则我们称抛物线
≠0,1,则我们称抛物线 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当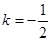 时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
查看答案和解析>>
科目:初中数学 来源:2011-2012年浙江省金华市上学期九年级月考数学卷 题型:解答题
、(本题10分)我们知道,对于二次函数y=a(x+m)2+k的图像,可由函数y=ax2的图像 进行向左或向右平移一次、再向上或向下移一次平移得到,我们称函数y=ax2为“基本函数”,而称由它平移得到的二次函数y=a(x+m)2+k为“基本函数”y=ax2的“朋友函数”。左右、上下平移的路径称为朋友路径,对应点之间的线段距离 称为朋友距离。
称为朋友距离。
由此,我们所学的函数:二次函数y=ax2,函数y=kx和反比例函数 都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”。
都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”。
如一次函数y=2x-5是基本函数y=2x的朋友函数,由y=2x-5=2(x-1)-3朋友路径可以是向右平移1个单位,再向下平移3个单位,朋友距离= .
.
1.(1)探究一:小明同学经过思考后,为函数y=2x-5又找到了一条朋友路径为由基本函数y=2x先向 ,再向下平移7单位,相应的朋友距离为 。
2.(2)探究二:已知函数y=x2-6x+5,求它的基本函数,朋友路径,和相应的朋友距离。
3.(3)探究三:为函数 和它的基本函数
和它的基本函数 ,找到朋友路径,
,找到朋友路径,
并求相应的朋友距离。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com