
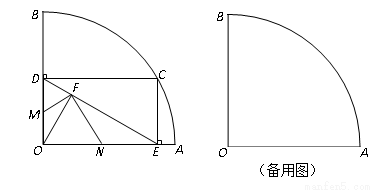
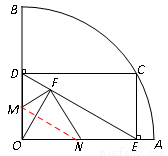
如图,扇形OAB的半径为4,圆心角∠AOB=90°,点C是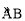 上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
(1)当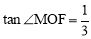 时,求
时,求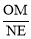 的值;
的值;
(2)设OM=x,ON=y,当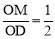 时,求y关于x 的函数解析式,并写出它的定义域;
时,求y关于x 的函数解析式,并写出它的定义域;
(3)在(2)的条件下,联结CF,当△ECF与△OFN相似时,求OD的长.
(1)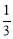 ;(2)
;(2)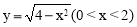 ;(3)
;(3)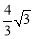 或
或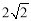 .
.
【解析】
试题分析:(1)由△MFO∽△NFE和 ,根据相似三角形的判定和性质,锐角三角函数定义, 即可求得结果.
,根据相似三角形的判定和性质,锐角三角函数定义, 即可求得结果.
(2)由△MFO∽△NFE和△ODF∽△EOF可得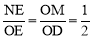 ,即
,即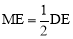 ,从而根据勾股定理可得出
,从而根据勾股定理可得出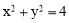 ,即
,即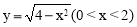 .
.
(3)分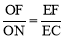 或
或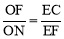 两种情况讨论即可.
两种情况讨论即可.
(1)由题意,得:∠MOF+∠FOE=90°,∠FEN+∠FOE=90° , ∴∠MOF=∠FEN .
由题意,得:∠MFO+∠OFN=90°,∠EFN+∠OFN=90° , ∴∠MFO=∠NFE.
∴△MFO∽△NFE.∴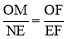 .
.
由∠FEN=∠MOF可得: , ∴
, ∴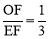 , ∴
, ∴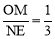 .
.
(2)∵△MFO∽△NFE , ∴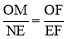 .
.
又易证得:△ODF∽△EOF , ∴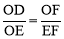 .
.
∴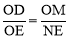 , ∴
, ∴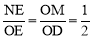 .
.
如图,连接MN,则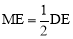 .
.
由题意,得四边形ODCE为矩形,∴DE=OC=4 .∴MN=2.
在Rt△MON中,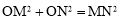 ,即
,即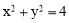 .
.
∴y关于x 的函数解析式为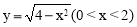 .
.
(3)由题意,可得: OE=2y,CE=OD=2x.
∴由题意,可得: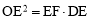 , ∴
, ∴ .
.
∵又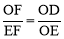 ,∴
,∴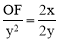 ,∴
,∴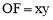 .
.
由题意,可得:∠NOF=∠FEC ,
∴由△ECF与△OFN相似,可得: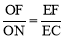 或
或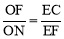 .
.
当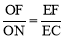 时,
时,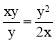 ,∴
,∴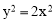 .
.
又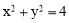 ,∴
,∴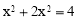 ,解得:
,解得: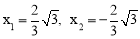 (舍去).
(舍去).
∴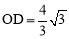 .
.
②当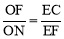 时,
时,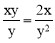 ,∴
,∴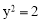 ,
,
又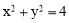 ,∴
,∴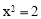 ,∴解得:
,∴解得: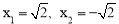 (舍去)
(舍去)
∴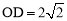 .
.
综上所述,OD=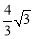 或
或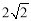 .
.
考点:1.双动点问题;2.矩形的性质;3.相似三角形的判定和性质;4.由实际问题列函数关系式;5.勾股定理;6.锐角三角函数定义;7.分类思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年中考数学章节复习测试四边形练习卷(解析版) 题型:填空题
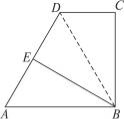
如图,在梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24.将该梯形折叠,点A恰好与点D重合,BE为折痕,那么AD的长度为_______________.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年中考数学章节复习测试分式练习卷(解析版) 题型:选择题
沿河的上游和下游各有一个港口A、B,货船在静水中的速度为a千米/时,水流的速度为b千米/时,那么一艘货船从A港口出发,在两港之间不停顿地往返一次所需的时间是
A.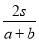 小时 B.
小时 B.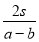 小时
小时
C.(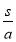 +
+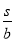 )小时 D.(
)小时 D.(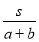 +
+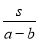 )小时
)小时
查看答案和解析>>
科目:初中数学 来源:2013-2014学年中考数学章节复习测试全等三角形练习卷(解析版) 题型:填空题
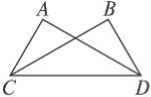
如图,AD⊥AC,BC⊥BD,要想使△ADC≌△BCD,小王添加了一个条件AC=BD,其依据为______________,你还可以加一个条件______________,依据为______________.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年中考数学章节复习测试二次函数练习卷(解析版) 题型:选择题
将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个,若这种商品的零售价在一定范围内每降价1元,其日销量就增加1个,为了获取最大利润则应降价
A.20元 B.15元
C.10元 D.5元
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市毕业生学业模拟考试数学试卷(解析版) 题型:选择题
已知一组数据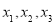 的平均数和方差分别为6和2,则数据
的平均数和方差分别为6和2,则数据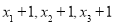 的平均数和方差分别是( )
的平均数和方差分别是( )
(A)6和2 (B)6和3 (C)7和2 (D)7和3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com