
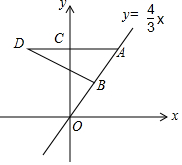
 如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限且在直线y=$\frac{4}{3}$x上,点B为线段OA的中点,过点A作y轴的垂线,点D是线段AC的延长线上的一点,连接BD.若∠OBD=3∠D,且CD=5,则直线BD的解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$.
如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限且在直线y=$\frac{4}{3}$x上,点B为线段OA的中点,过点A作y轴的垂线,点D是线段AC的延长线上的一点,连接BD.若∠OBD=3∠D,且CD=5,则直线BD的解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$. 分析 由∠OBD=3∠D结合外角的性质可得出∠A=2∠D,连接BC,根据直角三角形斜边上的中线等于底边的一半可得出BC=BA=BO,由等边对等角可得出∠A=∠BCA,结合三角形外角的性质可得出∠D=∠DBC,进而可得出BC=CD=5,由点A在第一象限且在直线y=$\frac{4}{3}$x上,设出点A的坐标为(x,$\frac{4}{3}$x),利用勾股定理可求出x值,进而得出点A的坐标,结合点B为线段OA的中点以及AC⊥y轴,可得出点B、D的坐标,再根据点B、D的坐标,利用待定系数法可求出直线BD的解析式.
解答 解:∵∠OBD=∠D+∠A,∠OBD=3∠A,
∴∠A=2∠D.
连接BC,如图所示.
∵△OAC为直角三角形,点B为线段OA的中点,
∴BC=BA=BO,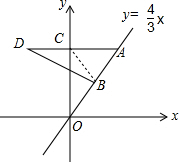
∴∠A=∠BCA.
∵∠BCA=∠D+∠DBC,
∴∠D=∠DBC,
∴CB=CD=5,OA=2BC=10.
设点A的坐标为(x,$\frac{4}{3}$x),则AC=x,OC=$\frac{4}{3}$x,
∵OA2=OC2+AC2,即102=x2+($\frac{4}{3}$x)2,
解得:x=6或x=-6(舍去),
∴点A的坐标为(6,8),
∴点B的坐标为(3,4),点D的坐标为(-5,8).
设直线BD的解析式为y=kx+b,
将点B(3,4)、D(-5,8)代入y=kx+b,
$\left\{\begin{array}{l}{3k+b=4}\\{-5k+b=8}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{11}{2}}\end{array}\right.$,
∴直线BD的解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$.
故答案为:y=-$\frac{1}{2}$x+$\frac{11}{2}$.
点评 本题考查了待定系数法求一次函数解析式、一次函数图象上点的坐标特征、等腰三角形的性质、勾股定理、直角三角形的性质以及三角形外角的性质,利用勾股定理求出点A的坐标是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图 A(0,-4)、B(-2,0),M为直线l1:x=-1上一点,N为直线l2:y=x+3上一点.若以A、B、M、N为顶点的四边形是平行四边形,求所有满足条件的点N的坐标;
如图 A(0,-4)、B(-2,0),M为直线l1:x=-1上一点,N为直线l2:y=x+3上一点.若以A、B、M、N为顶点的四边形是平行四边形,求所有满足条件的点N的坐标;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 端午节是我国四大传统文化节日之一,为每年的农历五月初五,自古以来端午节便有划龙舟及食粽等习俗.重庆某大型超市为了了解市民对“蛋黄粽”的喜好程度,特意在三峡广场做了试吃及问卷调查活动,将市民对“蛋黄粽”的喜好程度分为“A非常喜欢”、“B比较喜欢”、“C感觉一般”、“D不太喜欢”四个等级,并将四个等级分别计分为:A等级10分,B等级7分,C等级5分,D等级2分,根据调查结果绘制出如图所示的条形统计图,请问“蛋黄粽”的平均分是7分.
端午节是我国四大传统文化节日之一,为每年的农历五月初五,自古以来端午节便有划龙舟及食粽等习俗.重庆某大型超市为了了解市民对“蛋黄粽”的喜好程度,特意在三峡广场做了试吃及问卷调查活动,将市民对“蛋黄粽”的喜好程度分为“A非常喜欢”、“B比较喜欢”、“C感觉一般”、“D不太喜欢”四个等级,并将四个等级分别计分为:A等级10分,B等级7分,C等级5分,D等级2分,根据调查结果绘制出如图所示的条形统计图,请问“蛋黄粽”的平均分是7分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
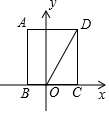 如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2$\sqrt{3}$,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是( )
如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2$\sqrt{3}$,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是( )| A. | (-$\sqrt{3}$,1) | B. | (-1,$\sqrt{3}$) | C. | (-1,$\sqrt{3}$)或(1,-$\sqrt{3}$) | D. | (-$\sqrt{3}$,1)或(1,-$\sqrt{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com