
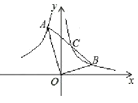
【题目】已知,如图点 A 、B 分别在反比例函数![]() 和
和![]() 上,OA OB ,连接 AB 与
上,OA OB ,连接 AB 与![]() 交于点C ,若C 为 AB 中点,则 SOAB =_____.
交于点C ,若C 为 AB 中点,则 SOAB =_____.
【答案】![]()
【解析】
过点A作AE⊥x轴于点E,过点B作BD⊥x轴于点D,则△AOE∽△OBD,根据相似三角形的性质结合反比例函数k的几何意义可得出![]() ,得到△OBC是等边三角形,BC=OB,点B,C关于直线y=x对称,设B(m,
,得到△OBC是等边三角形,BC=OB,点B,C关于直线y=x对称,设B(m,![]() ),则
),则![]() ,由两点间的距离公式得到
,由两点间的距离公式得到![]() ,
,![]() ,列出方程
,列出方程![]() 求解,再把所得的解代入三角形面积代数式中计算可得出
求解,再把所得的解代入三角形面积代数式中计算可得出![]() .
.
解:过点A作AE⊥x轴于点E,过点B作BD⊥x轴于点D,
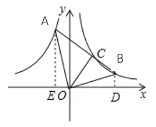
∵OA OB则易证△AOE∽△OBD
A 、B 分别在反比例函数![]() 和
和![]() 上,则SOAE=
上,则SOAE=![]() , SOBD=
, SOBD=![]() ,
,
![]()
∴∠OBA=60°
∵C 为 AB 中点,
∴△OBC是等边三角形,BC=OB
∵![]() 关于y=x对称,
关于y=x对称,
∴点B,C关于直线y=x对称
设B(m,![]() ),则
),则![]()
![]() ,
,![]()
∴![]()
解得:![]()
![]()
![]()
将![]() 代入,化简得
代入,化简得
![]()


科目:初中数学 来源: 题型:
【题目】(6分)如图①所示,将直尺摆放在三角板ABC上,使直尺与三角板的边分别交于点D,E,F,G,量得∠CGD=42°。

(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示.点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
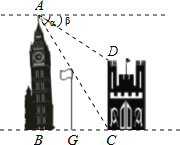
【题目】如图所示,在两建筑物之间有一高为15米的旗杆,从高建筑物的顶端A点经过旗杆顶点恰好看到矮建筑物的底端墙角C点,且俯角a为60°,又从A点测得矮建筑物左上角顶端D点的俯角β为30°,若旗杆底部点G为BC的中点(点B为点A向地面所作垂线的垂足)则矮建筑物的高CD为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l : y kx b k 0 与曲线有 n 个交点,则称直线l 为曲线的“ n 阶共生直线”,交点称为它们的“共生点”.
(1)若直线 y kx b k 0与某曲线的一个“共生点”为 P m, 2m 1,试判断此“共生点”不可能位于第几象限,请说明理由.
(2)若直线 l : y kx 2k k 0 与 x 、 y 轴分别交于 A 、 B 两点,且直线 l 为反比例函数y=![]() 的“ 2阶共生直线”,且“共生点”为C、D
的“ 2阶共生直线”,且“共生点”为C、D![]() ,求k的取值范围,试证明此时不论 k 取何值,总有 AC BD 成立.
,求k的取值范围,试证明此时不论 k 取何值,总有 AC BD 成立.
(3)若直线l : y kx 2k k 0 与 x 轴交于点 A ,且直线l 为抛物线 y x2 2x 1的“2 阶共生直线”,且“共生点”为 P 、Q xP xQ ,若 AQ 3AP ,求 k 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
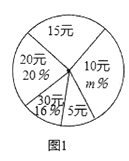
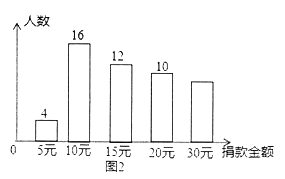
【题目】为了帮助贫困留守儿童,弘扬扶贫济困的传统美德,某校团委在学校举行“送温暖,献爱心”捐款活动,全校2000名学生都积极参与了该次活动.为了解捐款情况,随机调查了该校部分学生的捐款金额,并用得到的数据绘制出如下统计图1和图2,请根据相关信息,解答下列问题:
(I)本次接受随机抽样调查的学生人数为_________________,图1中m的值是_________________.
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校本次活动捐款金额超过20元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
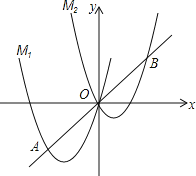
【题目】如图,将抛物线M1:y=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线y=x与M1的一个交点记为A,与M2的一个交点记为B,点A的横坐标是﹣3.
(1)求a的值及M2的表达式;
(2)点C是线段AB上的一个动点,过点C作x轴的垂线,垂足为D,在CD的右侧作正方形CDEF.
①当点C的横坐标为2时,直线y=x+n恰好经过正方形CDEF的顶点F,求此时n的值;
②在点C的运动过程中,若直线y=x+n与正方形CDEF始终没有公共点,求n的取值范围(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
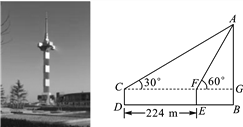
【题目】盐城电视塔是我市标志性建筑之一.如图,在一次数学课外实践活动中,老师要求测电视塔的高度AB.小明在D处用高1.5 m的测角仪CD,测得电视塔顶端A的仰角为30°,然后向电视塔前进224 m到达E处,又测得电视塔顶端A的仰角为60°.求电视塔的高度AB.( ![]() 取1.73,结果精确到0.1 m)
取1.73,结果精确到0.1 m)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com