
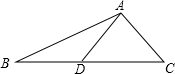
 如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=102°,则∠ADC=52度.
如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=102°,则∠ADC=52度.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 类型 | 进价(元/盏) | 售价(元/盏) |
| A型 | 40 | 60 |
| B型 | 50 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.1742 | B. | 3.174 | C. | 3.175 | D. | 3.1743 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
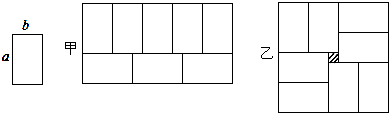
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
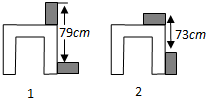 利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )
利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )| A. | 73cm | B. | 74cm | C. | 75cm | D. | 76cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{m}^{2}n}{4}$不是整式 | B. | -$\frac{3abc}{2}$的系数是-3,次数是3 | ||
| C. | 3是单项式 | D. | 多项式2x2y-xy是五次二项式 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com