
【题目】(1)补充完整:
如图1,在正方形ABCD中,E、F分别为DC、BC边上的点,且满足∠EAF=45°,连结EF,试说明DE+BF=EF.

解:将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合.由旋转可得AB=AD,GB=ED,∠1=∠2,∠ABG=∠D=90°.
∴∠ABG+∠ABF=90°+90°=180°.
∴点G、B、F在同一条直线上.
∵∠EAF=45°,
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°
∵∠1=∠2,
∴∠1+∠3=45°.
∴∠GAF=∠ .
又∵AG=AE,AF=AF.
∴△GAF≌ .
∵ =EF.
∴DE+BF=BG+BF=GF=EF.
(2)类比引申:
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°,若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,试猜想BD、DE、EC满足的等量关系,并写出推理过程.
【答案】(1) EAF,△EAF,GF;(2)∠B+∠D=180°;(3)BD2+CE2=DE2.
【解析】
(1)把△AEE绕点A顺时针旋转90°至△ABG,可使AB与AD重合,证出△AFG≌△AFE,根据全等三角形的性质得出EF=FG,即可得出答案;
(2)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFE≌△AFG,根据全等三角形的性质得出EF=FG,即可得出答案;
(3)把△ACE旋转到ABF的位置,连接DF,证明△AFE≌△AFG(SAS),则EF=FG,∠C=∠ABF=45°,△BDF是直角三角形,根据勾股定理即可作出判断.
(1)将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合.由旋转可得AB=ADMBGD,∠1=∠2,∠ABG=∠D=90°.
∴∠ABG+∠ABF=90°+90°=180°.
∴点G、B、F在同一条直线上.
∵∠EAF=45°,
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45,
∵∠1=∠2,
∴∠1+∠3=45°.
∴∠GAF=∠EAF.
又∵AG=AE,AF=AF.
∴△GAF≌△EAF.
∵GF=EF.
∴DE+BF=BG+BF=GF=EF,
故答案为EAF,△EAF,GF
(2)∠B+∠D=180°时,EF=BE+DF;
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图2,

∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC+∠B=180°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中,

∴△AFE≌△AFG(SAS),
∴EF=FG,
即:EF=BE+DF,
故答案为:∠B+∠ADC=180°;
(3)BD2+CE2=DE2.
理由是:把△ACE旋转到ABF的位置,连接DF,则∠FAB=∠CAE.

∵∠BAC=90°,∠DAE=45°,
∴∠BAD+∠CAE=45°,
又∵∠FAB=∠CAE,
∴∠FAD=∠DAE=45°,
则在△ADF和△ADE中,

∴△ADF≌△ADE,
∴DF=DE,∠C=∠ABF=45°,
∴∠BDF=90°,
∴△BDF是直角三角形,
∴BD2+BF2=DF2,
∴BD2+CE2=DE2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知分式: ![]()
(1)化简这个分式
(2)把分式A化简结果的分子与分母同时加上3后得到分式B,问:当a>2时,分式B的值较原来分式A的值是变大了还是变小了?试说明理由。
(3)若A的值是整数,且a也为整数,求出所有符合条件a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+![]() ,PA=
,PA=![]() ,则:
,则:
①线段PB= ,PC= ;
②猜想:PA2,PB2,PQ2三者之间的数量关系为 ;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足![]() ,求
,求![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级在探究“将军饮马问题”时抽象出数学模型:
直线l同旁有两个定点A、B,在直线![]() 上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线
上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,则
,则![]() 与直线l的交点即为P,且PA+PB的最小值为
与直线l的交点即为P,且PA+PB的最小值为![]() .
.


请利用上述模型解决下列问题:
(1)几何应用:如图2,△ABC中,∠C=90°,AC=BC=2,E是AB的中点,P是BC边上的一动点,则PA+PE的最小值为 ;
(2)代数应用:求代数式![]() +
+![]() (0≤x≤3)的最小值.
(0≤x≤3)的最小值.
(3)几何拓展:如图3,△ABC中,AC=2,∠A=30°,若在AB、AC上各取一点M、N使BM+MN的值最小,最小值是 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中: ①△BDE是等边三角形; ②AE∥BC; ③△ADE的周长是9; ④∠ADE=∠BDC.其中正确的序号是( )
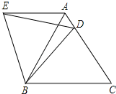
A.②③④B.①②④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,先描出点![]() ,点
,点![]() .
.
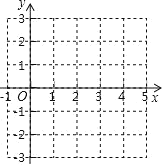
(1)描出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的位置,写出
的位置,写出![]() 的坐标 ;
的坐标 ;
(2)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);
(3)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() (保留作图痕迹).
(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解决问题:
![]() 如图
如图![]() 等边
等边![]() 内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求
内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求![]() 的度数.为了解决本题,我们可以将
的度数.为了解决本题,我们可以将![]() 绕顶点A旋转到
绕顶点A旋转到![]() 处,此时
处,此时![]() ≌
≌![]() ,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出
,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出![]() ______;
______;
![]() 基本运用
基本运用
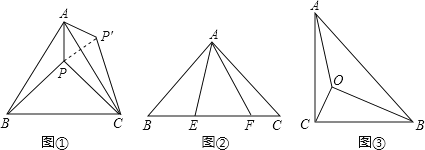
请你利用第![]() 题的解答思想方法,解答下面问题:已知如图
题的解答思想方法,解答下面问题:已知如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,E、F为BC上的点且
,E、F为BC上的点且![]() ,求证:
,求证:![]() ;
;
![]() 能力提升
能力提升
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点O为
,点O为![]() 内一点,连接AO,BO,CO,且
内一点,连接AO,BO,CO,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°, 点D在AB上,且CD=BD.

(1)求证:点D是AB的中点.
(2)以CD为对称轴将△ACD翻折至△A'CD,连接BA',若∠DBC=a,求∠CB A'的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com