
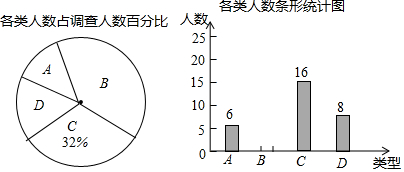
分析 (1)首先求出总人数,再求出B类的人数即可求出扇形统计图中B类所对应的扇形圆心角的度数,进而可补全全条形统计图;
(2)(2)利用图表得出从4为同学中选两位同学的等可能结果共有12种,进而得出符合要求的结果,求出概率即可.
解答 解:
(1)
由统计表可知总人数=16÷32%=50(人),所以B类的人数=50-6-16-8=20(人),
所以扇形统计图中B类所对应的扇形圆心角的度数=$\frac{20}{50}$×360°=144°,
故答案为:144.
补全统计表如图所示: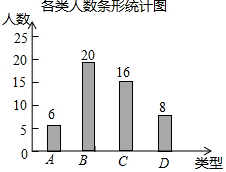
(2)列表如下:
| 第一次所选 第二次所选 | 男 | 男 | 男 | 女 |
| 男 | ▲ | 男,男 | 男,男 | 男,女 |
| 男 | 男,男 | ▲ | 男,男 | 女,男 |
| 男 | 男,男 | 男,男 | ▲ | 女,男 |
| 女 | 女,男 | 女,男 | 女,男 | ▲ |
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
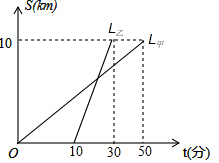 甲骑自行车,乙乘公交车,从同一地点出发沿相同路线前往某校参加绘画比赛,图中l甲、l乙分别表示甲、乙两人前往目的地所行使的路程s(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶0.3千米.
甲骑自行车,乙乘公交车,从同一地点出发沿相同路线前往某校参加绘画比赛,图中l甲、l乙分别表示甲、乙两人前往目的地所行使的路程s(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶0.3千米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{1}$=±1 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\root{3}{-125}$=-5 | D. | $\sqrt{-1}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com