
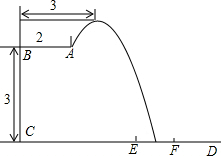
 2016年里约奥运会,中国跳水队赢得8个项目中的7块金牌,优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.
2016年里约奥运会,中国跳水队赢得8个项目中的7块金牌,优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.分析 (1)根据抛物线顶点坐标M(3,4),可设抛物线解析为:y=a(x-3)2+4,将点A(2,3)代入可得;
(2)在(1)中函数解析式中令y=0,求出x即可;
(3)若跳水运动员在区域EF内(含点E,F)入水达到训练要求,则在函数y=a(x-3)2+k中当x=$\frac{19}{4}$米,y>0,当x=$\frac{21}{4}$米时y<0,解不等式即可得.
解答 解:(1)如图所示: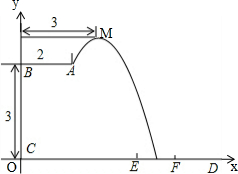
根据题意,可得抛物线顶点坐标M(3,4),A(2,3)
设抛物线解析为:y=a(x-3)2+4,
则3=a(2-3)2+4,
解得:a=-1,
故抛物线解析式为:y=-(x-3)2+4;
(2)由题意可得:当y=0,则0=-(x-3)2+4,
解得:x1=1,x2=5,
故抛物线与x轴交点为:(5,0),
当k=4时,求运动员落水点与点C的距离为5米;
(3)根据题意,抛物线解析式为:y=a(x-3)2+k,
将点A(2,3)代入可得:a+k=3,即a=3-k
若跳水运动员在区域EF内(含点E,F)入水,
则当x=$\frac{19}{4}$时,y=$\frac{49}{16}$a+k≥0,即$\frac{49}{16}$(3-k)+k≥0,
解得:k≤$\frac{49}{11}$,
当x=$\frac{21}{4}$时,y=$\frac{81}{16}$a+k≤0,即$\frac{81}{16}$(3-k)+k≤0,
解得:k≥$\frac{243}{65}$,
故$\frac{243}{65}$≤k≤$\frac{49}{11}$.
点评 此题主要考查了二次函数的应用,根据题意利用顶点式求出二次函数解析式是解题基础,判断入水的位置对应的抛物线上点的坐标特点是解题关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
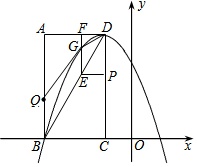 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(-3,4)、B(-3,0)、C(-1,0).以D为顶点的抛物线y=ax2+bx+c过点B.动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒.过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(-3,4)、B(-3,0)、C(-1,0).以D为顶点的抛物线y=ax2+bx+c过点B.动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒.过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
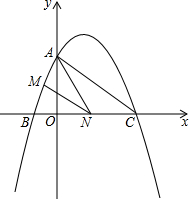 如图,已知二次函数y=ax2+$\frac{3}{2}$x+c的图象与y轴交于点A(0,4),与x轴交于点B,C,点C的坐标为(8,0),连接AC、AC.
如图,已知二次函数y=ax2+$\frac{3}{2}$x+c的图象与y轴交于点A(0,4),与x轴交于点B,C,点C的坐标为(8,0),连接AC、AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
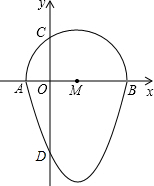 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$.
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
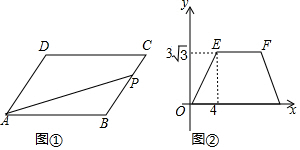
| A. | 7 | B. | 8 | C. | 4+2$\sqrt{3}$ | D. | 4+$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com