
【题目】如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,D,E分别是AB,AC边的中点,将△ABC绕点B顺时针旋转60°到△A′BC′的位置,则整个旋转过程中线段DE所扫过部分的面积(即图中阴影部分面积)为_____.

【答案】![]() .
.
【解析】
根据30°角所对的直角边等于斜边的一半求出AB的长度,再根据勾股定理求出AC的长度,然后根据中点定义求出DB、CE的长度,再利用勾股定理求出BE的长度,然后根据旋转变换的性质可得阴影部分的面积等于以BE为半径的扇形面积减去以DB为半径的扇形的面积,然后列式进行计算即可得解.
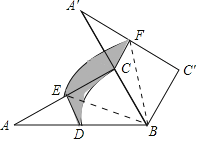
解:连接BE、BF,如右图所示,
∵Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,
∴AB =2BC=12,∴AC=6![]() ,
,
∵D,E分别是AB,AC边的中点,
∴EC=![]() AC=3
AC=3![]() ,BD=BC=
,BD=BC=![]() AB=6,
AB=6,
在Rt△BCE中,根据勾股定理得:BE=3![]() ,
,
∴图中阴影部分面积是:![]() -
-![]() =
=![]() ,
,
故答案为:![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】点![]() 的“
的“![]() 值”定义如下:若点
值”定义如下:若点![]() 为圆上任意一点,线段
为圆上任意一点,线段![]() 长度的最大值与最小值之差即为点
长度的最大值与最小值之差即为点![]() 的“
的“![]() 值”,记为
值”,记为![]() .特别的,当点
.特别的,当点![]() ,
, ![]() 重合时,线段
重合时,线段![]() 的长度为0.
的长度为0.
当⊙![]() 的半径为2时:
的半径为2时:
(1)若点![]() ,
, ![]() ,则
,则![]() _________,
_________, ![]() _________;
_________;
(2)若在直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求出点
,求出点![]() 的横坐标;
的横坐标;
(3)直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于点
轴分别交于点![]() ,
, ![]() .若线段
.若线段![]() 上存在点
上存在点![]() ,使得
,使得![]() ,请你直接写出
,请你直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,点A(1,5)和点B(m,1)均在反比例函数y=![]() 图象上.
图象上.
(1)求m,k的值;
(2)设直线AB与x轴交于点C,求△AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.
(1)求证:∠PCA=∠ABC.
(2)过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若cos∠P=![]() ,CF=10,求BE的长
,CF=10,求BE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y=![]() 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题:
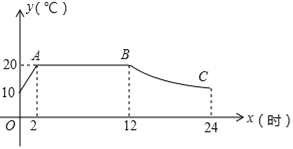
(1)求0到2小时期间y随x的函数解析式;
(2)恒温系统在一天内保持大棚内温度不低于15℃的时间有多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx﹣3,有下列结论:
①它的图象与x轴有两个交点;
②如果当x≤﹣1时,y随x的增大而减小,则m=﹣1;
③如果将它的图象向左平移3个单位后过原点,则m=1;
④如果当x=2时的函数值与x=8时的函数值相等,则m=5.
其中一定正确的结论是_______.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
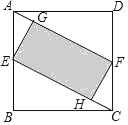
A. y=3![]() x2 B. y=4
x2 B. y=4![]() x2 C. y=8x2 D. y=9x2
x2 C. y=8x2 D. y=9x2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com