
【题目】△ABC内接于⊙O,AT切⊙O于点A,AB=BC,且AT∥BC.
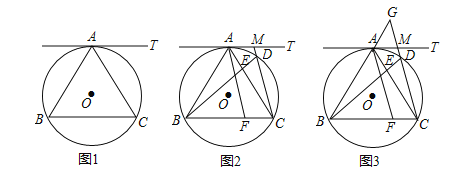
(1)如图1,求证:△ABC是等边三角形;
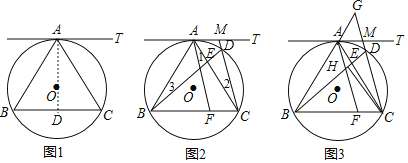
(2)如图2,点M在射线AT上,连接CM交⊙O于点D,连接BD交AC于点E,AF∥CM交BC于点F,求证:AE=CF;
(3)如图3,在(2)的条件下,延长BA、CM交于点G,若BD=40,CD=25,求AG的长.
【答案】(1)详见解析;(2)详见解析;(3)21
【解析】
(1)连接AO,延长AO交BC于D,如图1,利用切线的性质得OA⊥BC,则AD⊥BC,利用垂径定理可判断AD垂直平分BC,所以AB=AC,然后根据等边三角形的定义可得到结论;
(2)如图2,先利用等边三角形的性质得∠ABC=∠BAC=∠ACB=60°,再∠1=∠3,然后利用“ASA”可证明△ABE≌△CAF,从而得到AE=CF;
(3)作CH⊥BD于H,如图3,利用圆周角得到∠BDC=∠BAC=60°,利用含30度的直角三角形三边的关系可计算出DH=![]() ,CH=
,CH=![]() ,则BH=
,则BH=![]() ,再利用勾股定理计算出BC=35,接着证明△GAM∽△GBC,利用相似比得到AM=
,再利用勾股定理计算出BC=35,接着证明△GAM∽△GBC,利用相似比得到AM=![]() ,证明△GAM∽△BDC,利用相似比得到AM=
,证明△GAM∽△BDC,利用相似比得到AM=![]() AG,所以
AG,所以![]() =
=![]() AG,然后解方程可得到AG的长.
AG,然后解方程可得到AG的长.
(1)证明:连接AO,延长AO交BC于D,如图1,
∵AT切⊙O于点A,
∴OA⊥BC,
∵AT∥BC,
∴AD⊥BC,
∴BD=CD,
即AD垂直平分BC,
∴AB=AC,
而AB=BC,
∴AB=BC=AC,
∴△ABC是等边三角形;
(2)证明:如图2,
∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∵AF∥CM,
∴∠1=∠2,
而∠2=∠3,
∴∠1=∠3,
在△ABE和△CAF中
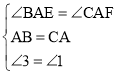 ,
,
∴△ABE≌△CAF,
∴AE=CF;
(3)解:作CH⊥BD于H,如图3,
∵∠BDC=∠BAC=60°,
∴DH=![]() CD=
CD=![]() ,
,
∴CH=![]() DH=
DH=![]() ,BH=BD﹣DH=40﹣
,BH=BD﹣DH=40﹣![]() =
=![]() ,
,
在Rt△BCH中,BC=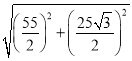 =35,
=35,
∵AM∥BC,
∴△GAM∽△GBC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AM=![]() ,
,
∵AM∥BC,
∴∠GAM=∠ABC=60°,∠GMA=∠GCB,
∴∠BDC=∠GAM,∠DCB=∠GMA,
∴△GAM∽△BDC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AM=![]() AG,
AG,
∴![]() =
=![]() AG,
AG,
∴AG=21.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
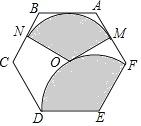
【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了如下不完整的统计图:

根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为3000人,请估计成绩是“优”和“良”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
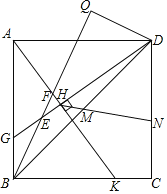
【题目】如图,Q为正方形ABCD外一点,连接BQ,过点D作DQ⊥BQ,垂足为Q,G、K分别为AB、BC上的点,连接AK、DG,分别交BQ于F、E,AK⊥DG,垂足为点H,AF=5,DH=8,F为BQ中点,M为对角线BD的中点,连接HM并延长交正方形于点N,则HN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像如图所示,对称轴为直线
的图像如图所示,对称轴为直线![]() ,则下列结论正确的有( )
,则下列结论正确的有( )
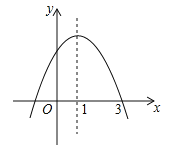
①![]() ;②方程
;②方程![]() 的两个根是
的两个根是![]() ,
,![]() ;
;
③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
A.①②B.②③C.①④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁岭市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示:
(1)求y与x之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
(3)该干果每千克降价多少元时,商贸公司获利最大?最大利润是多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com