
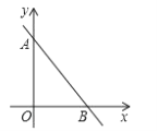
【题目】如图,在直角坐标系xOy中,O为坐标原点,直线AB分别与y轴,x轴交于A(0,4),B(3,0)两点.
(1)尺规作图:在x轴上求作一点C,使得△ABC是以![]() 为顶角的等腰三角形,并在图中标明相应字母;(保留作图痕迹,不写作法)
为顶角的等腰三角形,并在图中标明相应字母;(保留作图痕迹,不写作法)
(2)在(1)的条件下,求点C的坐标.
 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
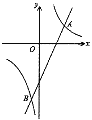
【题目】如图,在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交点为
的图象交点为![]() ,
,![]() .
.
(1)求反比例函数与一次函数的解析式及![]() 点坐标;
点坐标;
(2)若![]() 是
是![]() 轴上的点,且满足
轴上的点,且满足![]() 的面积为10,求
的面积为10,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
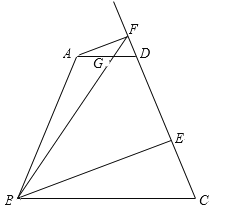
【题目】如图,在梯形ABCD中,AD // BC,AB = CD,AD = 5,BC = 15,![]() .E为射线CD上任意一点,过点A作AF // BE,与射线CD相交于点F.联结BF,与直线AD相交于点G.设CE = x,
.E为射线CD上任意一点,过点A作AF // BE,与射线CD相交于点F.联结BF,与直线AD相交于点G.设CE = x,![]() .
.
(1)求AB的长;
(2)当点G在线段AD上时,求y关于x的函数解析式,并写出函数的定义域;
(3)如果![]() ,求线段CE的长.
,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校运动会的立定跳远和1分钟跳绳两个单项比赛分成预赛和决赛两个阶段.下表为参加这两项比赛的10名学生的预赛成绩:
学生编号 成绩 项目 | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1分钟跳绳(单位:次) | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
在这10名学生中,同时进入两项决赛的只有6人,进入立定跳远决赛的有8![]() 的值是__________.
的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C1:y=ax2﹣2ax﹣3a(a≠0)和点A(0,﹣3),将点A向右平移2个单位,再向上平移5个单位,得到点B.
(1)求点B的坐标;
(2)求抛物线C1的对称轴;
(3)把抛物线C1沿x轴翻折,得到一条新抛物线C2,抛物线C2与抛物线C1组成的图象记为G,若图象G与线段AB恰有一个交点时,结合图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
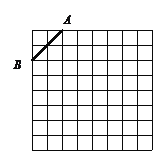
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)在第二象限内的格点(网格线的交点)上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,求C点坐标和△ABC的周长(结果保留根号);
(3)画出△ABC以点C为旋转中心,旋转180°后的△DEC,连结AE和BD,试说明四边形ABDE是什么特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在相同条件下完成了10次射击训练,两人的成绩如图所示。

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 方差/环 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根据训练成绩,你认为选派哪一名队员参赛更好?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
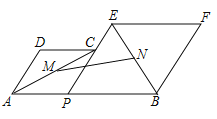
【题目】如图,已知![]() ,
,![]() 为线段
为线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() ,
,![]() 为边在
为边在![]() 的同侧作菱形
的同侧作菱形![]() 和菱形
和菱形![]() .点
.点![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() ,
,![]() 、
、![]() 分别是对角线
分别是对角线![]() 、
、![]() 的中点.当点
的中点.当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() 、
、![]() 之间的距离最短为_______.
之间的距离最短为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com