
【题目】如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE,分别交AC、AD于点F、G,连接OG,则下列结论:①OG=![]() AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )
AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )
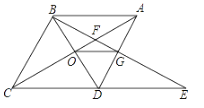
A. ①③B. ①③④C. ①②③D. ②②④
【答案】A
【解析】
由AAS证明△ABG≌△DEG,得出AG=DG,证出OG是△ACD的中位线,得出OG=![]() CD=
CD=![]() AB,①正确;先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,③正确;由菱形的性质得得出△ABG≌△BDG≌△DEG,由SAS证明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正确;证出OG是△ABD的中位线,得出OG//AB,OG=
AB,①正确;先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,③正确;由菱形的性质得得出△ABG≌△BDG≌△DEG,由SAS证明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正确;证出OG是△ABD的中位线,得出OG//AB,OG=![]() AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;④不正确;即可得出结果.
AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;④不正确;即可得出结果.
解:四边形ABCD是菱形,

在△ABG和△DEG中,
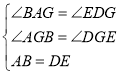
∴△ABG≌△DEG(AAS),
∴.AG=DG,
∴OG是△ACD的中位线,
∴OG=![]() CD=
CD=![]() AB,①正确;
AB,①正确;
∵AB//CE,AB=DE,
∴四边形ABDE是平行四边形,
∴∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,③正确;
∴AD⊥BE,
由菱形的性质得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中,
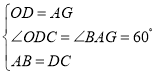
∴△ABG≌△DCO
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,则②不正确。
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG∥AB,OG=![]() AB,
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∴△GOD的面积=![]() △ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△AOG的面积=△BOG的面积,
∴ S四边形ODGF=S△ABF;④不正确;
故答案为:A.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】下面两个多位数1248624…… ,6248624…… ,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是( )
A. 495 B. 497 C. 501 D. 503
查看答案和解析>>
科目:初中数学 来源: 题型:
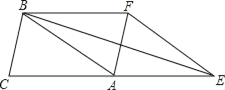
【题目】如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.
(1)求四边形CEFB的面积;
(2)试判断AF与BE的位置关系,并说明理由;
(3)若∠BEC=15°,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察数轴,请回答:
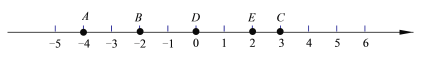
(1)点C与点D的距离为______ ,点B与点D的距离为______ ;
(2)点B与点E的距离为______ ,点A与点C的距离为______ ;
发现:在数轴上,如果点M与点N分别表示数m,n,则他们之间的距离可表示为 ______(用m,n表示)
(3)利用发现的结论解决下列问题: 数轴上表示x的点P与B之间的距离是1,则 x 的值是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若甲、乙两人同时从某地出发,沿着同一个方向行走到同一个目的地,其中甲一半的路程以a(km/h)的速度行走,另一半的路程以b(km/h)的速度行走;乙一半的时间以a(km/h)的速度行走,另一半的时间以b(km/h)的速度行走(a≠b),则先到达目的地的是( )
A. 甲B. 乙
C. 同时到达D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形![]() 的顶点
的顶点![]() 在坐标原点,顶点
在坐标原点,顶点![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() 为边
为边![]() 的中点,
的中点,![]() 是边
是边![]() 上的一个动点,当
上的一个动点,当![]() 的周长最小时,点
的周长最小时,点![]() 的坐标为_________.
的坐标为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1
(1)当点A1落在AC上时
①如图1,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
②如图2,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO;
(2)如图3,当A1D1过点C时.若BC=5,CD=3,直接写出A1A的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
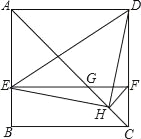
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论:
①EG=DF;②∠AEH+∠ADH=180 ;③△EHF≌△DHC;④若![]() ,则3S△EDH=13S△DHC,其中结论正确的有___________.
,则3S△EDH=13S△DHC,其中结论正确的有___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com